题目内容
下列各式中,值为-
的是( )
| ||
| 2 |
| A、2sin15°cos15° |
| B、cos215°-sin215° |
| C、2sin215°-1 |
| D、sin215°+cos215° |
分析:A、利用二倍角的正弦函数公式及特殊角的三角函数值求出原式的值,即可作出判断;
B、根据二倍角的余弦函数公式及特殊角的三角函数值求出原式的值,即可作出判断;
C、把所求的式子提取-1后,利用二倍角的余弦函数公式及特殊角的三角函数值求出原式的值,即可作出判断;
D、根据同角三角函数间的基本关系求出值,作出判断.
B、根据二倍角的余弦函数公式及特殊角的三角函数值求出原式的值,即可作出判断;
C、把所求的式子提取-1后,利用二倍角的余弦函数公式及特殊角的三角函数值求出原式的值,即可作出判断;
D、根据同角三角函数间的基本关系求出值,作出判断.
解答:解:A、2sin15°cos15°=sin30°=
,本选项错误;
B、cos215°-sin215°=cos30°=
,本选项错误;
C、2sin215°-1=-(1-2sin215°)=-cos30°=-
,本选项正确;
D、sin215°+cos215°=1,本选项错误,
故选C
| 1 |
| 2 |
B、cos215°-sin215°=cos30°=
| ||
| 2 |
C、2sin215°-1=-(1-2sin215°)=-cos30°=-
| ||
| 2 |
D、sin215°+cos215°=1,本选项错误,
故选C
点评:此题考查了二倍角的正弦、余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式的结构特点是解本题的关键.

练习册系列答案
相关题目
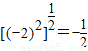 ;
; 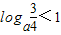 则a
则a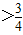 ;
; ];
];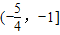 .
.