题目内容
如图，已知| OA |
| a |
| OB |
| b |
（1）用
| a |
| b |
| MN |
（2）设|
| a |
| b |
| a |
| b |
| MN |
| a |
| b |
分析：（1）由题意可得，AB是△SMN的中位线，故有
=2
=2（
-
），化简可得结果．
（2）利用两个向量垂直的性质可得
•（λ
+
）=0，化简可得-λ
2+
2+（λ-1）
•
=0，由此求得实数λ的值．
| MN |
| AB |
| OB |
| OA |
（2）利用两个向量垂直的性质可得
| MN |
| a |
| b |
| a |
| b |
| a |
| b |
解答：解：（1）由题意可得，AB是△SMN的中位线，故有
=2
=2（
-
）=2（
-
）．
（2）∵
⊥（λa+b），∴
•（λ
+
）=0，即 2（
-
）•（λ
+
）=0，
即-λ
2+
2+（λ-1）
•
=0，
∴-λ+4+1×2×cos30°（λ-1）=0，
解得 λ=
．
| MN |
| AB |
| OB |
| OA |
| b |
| a |
（2）∵
| MN |
| MN |
| a |
| b |
| b |
| a |
| a |
| b |
即-λ
| a |
| b |
| a |
| b |
∴-λ+4+1×2×cos30°（λ-1）=0，
解得 λ=
-1-3
| ||
| 2 |
点评：本题主要考查两个向量的数量积的运算，向量在几何中的应用，两个向量垂直的性质，属于中档题．
练习册系列答案
相关题目
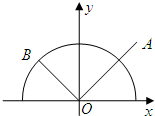如图，已知点A（1，1）和单位圆上半部分上的动点B．
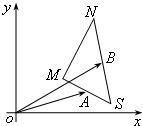如图，已知
如图，已知
如图，已知