题目内容

如图，已知
OA
=
p
，
OB
=
q
，
OC
=
r
且
AB
=2
BC

（1）试用
p
，
q
表示
r
，
（2）若A(
7
2
，
1
2
)，B(
5
2
，
3
2
)，求点C的坐标．
分析：（1）由题意可得
AB
=2
BC
，利用两个向量的加减法的法则，以及其几何意义可得
OC
=
OB
+
BC
=
OB
+
1
2
•
AB
=
3
2
OB
-
1
2
OA
=
3
2
•
q
-
1
2
p
．
（2）设点C的坐标为 （x，y），由
AB
=2
BC
，可得
2x-5=-1
2y-3=1
，解得x、y的值，即可求得点C的坐标．
解答：解：（1）∵已知
OA
=
p
，
OB
=
q
，
OC
=
r
，且
AB
=2
BC
，
∴
OC
=
OB
+
BC
=
OB
+
1
2
•
AB
=
3
2
OB
-
1
2
OA
=
3
2
•
q
-
1
2
p
．
（2）设点C的坐标为 （x，y），则
AB
=（-1，1），
BC
=（x-
5
2
，y-
3
2
），
∵
AB
=2
BC
，
∴
2x-5=-1
2y-3=1
，解得
x=2
y=2
，
故点C的坐标为 （2，2）．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量坐标形式的运算，属于中档题．
练习册系列答案
相关题目
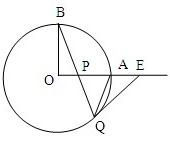21、如图，已知OA、OB是⊙O的半径，且OA⊥OB，P是线段OA上一点，直线BP交⊙O于点Q，过Q作⊙O的切线交直线OA于点E，求证：∠OBP+∠AQE=45°．
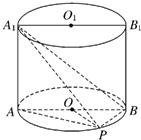精英家教网如图，已知点P在圆柱OO1的底面圆O上，AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB．
（1）求证：BP⊥A1P；
（2）若圆柱OO1的体积V=12π，OA=2，∠AOP=120°，求三棱锥A1-APB的体积．
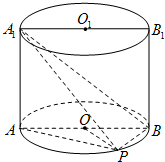精英家教网如图，已知点P在圆柱OO1的底面圆O上，AB为圆O的直径，圆柱OO1的表面积为20π，OA=2，∠AOP=120°．
（1）求异面直线A1B与AP所成角的大小；（结果用反三角函数值表示）
（2）求点A到平面A1PB的距离．
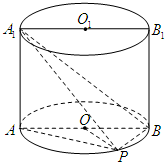如图，已知点P在圆柱OO1的底面圆O上，AB为圆O的直径，OA=2，∠AOP=120°，三棱锥A1-APB的体积为
8
3
3
．
（1）求圆柱OO1的表面积；
（2）求异面直线A1B与OP所成角的大小．  （结果用反三角函数值表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网