题目内容
对于函数f(x),若存在x∈R,使f(x)=x成立,则称x为f(x)的不动点.如果函数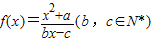 有且仅有两个不动点0、2,且
有且仅有两个不动点0、2,且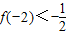 .
.(1)试求函数f(x)的单调区间;
(2)已知各项不为零的数列{an}满足
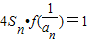 ,求证:
,求证: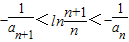 ;
;(3)设
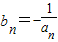 ,Tn为数列{bn}的前n项和,求证:T2008-1<ln2008<T2007.
,Tn为数列{bn}的前n项和,求证:T2008-1<ln2008<T2007.
【答案】分析:(1)利用函数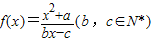 有且仅有两个不动点0、2,可得
有且仅有两个不动点0、2,可得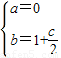 ,根据
,根据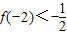 可确定c的范围,从而可确定c,b的值,进而可得函数解析式,利用导数法求函数f(x)的单调区间;
可确定c的范围,从而可确定c,b的值,进而可得函数解析式,利用导数法求函数f(x)的单调区间;
(2)由已知可得2Sn=an-an2,当n≥2时,2Sn-1=an-1-an-12,两式相减得(an+an-1)(an-an-1+1)=0,从而有an=-an-1或an-an-1=-1,进而可得an=-n,故待证不等式即为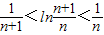 .再构造函数用函数的思想解决;
.再构造函数用函数的思想解决;
(3)由(2)可知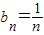 则
则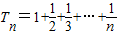 ,在
,在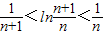 中令n=1,2,3,…,2007,并将各式相加,即可得证.
中令n=1,2,3,…,2007,并将各式相加,即可得证.
解答:解:(1)设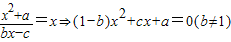
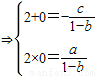 ∴
∴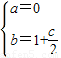 ∴
∴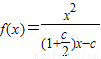
由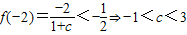
又∵b,c∈N*∴c=2,b=2
∴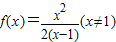 …(3分)
…(3分)
于是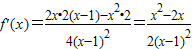
由f'(x)>0得x<0或x>2; 由f'(x)<0得0<x<1或1<x<2
故函数f(x)的单调递增区间为(-∞,0)和(2,+∞),
单调减区间为(0,1)和(1,2)…(4分)
(2)由已知可得2Sn=an-an2,当n≥2时,2Sn-1=an-1-an-12
两式相减得(an+an-1)(an-an-1+1)=0
∴an=-an-1或an-an-1=-1
当n=1时,2a1=a1-a12⇒a1=-1,若an=-an-1,则a2=1这与an≠1矛盾
∴an-an-1=-1∴an=-n…(6分)
于是,待证不等式即为 .
.
为此,我们考虑证明不等式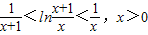
令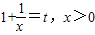 ,则t>1,
,则t>1,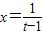
再令g(t)=t-1-lnt,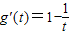 由t∈(1,+∞)知g'(t)>0
由t∈(1,+∞)知g'(t)>0
∴当t∈(1,+∞)时,g(t)单调递增∴g(t)>g(1)=0于是t-1>lnt
即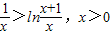 ①
①
令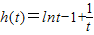 ,
,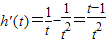 由t∈(1,+∞)知h'(t)>0
由t∈(1,+∞)知h'(t)>0
∴当t∈(1,+∞)时,h(t)单调递增∴h(t)>h(1)=0于是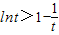
即 ②
②
由①、②可知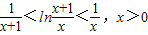 …(10分)
…(10分)
所以,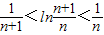 ,即
,即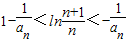 …(11分)
…(11分)
(3)由(2)可知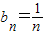 则
则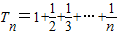
在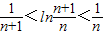 中令n=1,2,3,…,2007,并将各式相加得
中令n=1,2,3,…,2007,并将各式相加得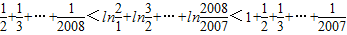
即T2008-1<ln2008<T2007…(14分)
点评:本题以函数为载体,考查新定义,考查函数解析式,考查数列与不等式,有较大的难度.
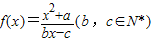 有且仅有两个不动点0、2,可得
有且仅有两个不动点0、2,可得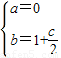 ,根据
,根据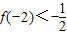 可确定c的范围,从而可确定c,b的值,进而可得函数解析式,利用导数法求函数f(x)的单调区间;
可确定c的范围,从而可确定c,b的值,进而可得函数解析式,利用导数法求函数f(x)的单调区间;(2)由已知可得2Sn=an-an2,当n≥2时,2Sn-1=an-1-an-12,两式相减得(an+an-1)(an-an-1+1)=0,从而有an=-an-1或an-an-1=-1,进而可得an=-n,故待证不等式即为
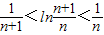 .再构造函数用函数的思想解决;
.再构造函数用函数的思想解决;(3)由(2)可知
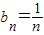 则
则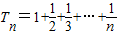 ,在
,在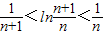 中令n=1,2,3,…,2007,并将各式相加,即可得证.
中令n=1,2,3,…,2007,并将各式相加,即可得证.解答:解:(1)设
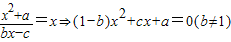
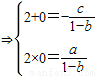 ∴
∴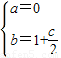 ∴
∴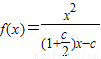
由
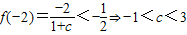
又∵b,c∈N*∴c=2,b=2
∴
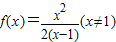 …(3分)
…(3分)于是
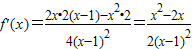
由f'(x)>0得x<0或x>2; 由f'(x)<0得0<x<1或1<x<2
故函数f(x)的单调递增区间为(-∞,0)和(2,+∞),
单调减区间为(0,1)和(1,2)…(4分)
(2)由已知可得2Sn=an-an2,当n≥2时,2Sn-1=an-1-an-12
两式相减得(an+an-1)(an-an-1+1)=0
∴an=-an-1或an-an-1=-1
当n=1时,2a1=a1-a12⇒a1=-1,若an=-an-1,则a2=1这与an≠1矛盾
∴an-an-1=-1∴an=-n…(6分)
于是,待证不等式即为
 .
.为此,我们考虑证明不等式
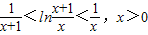
令
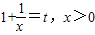 ,则t>1,
,则t>1,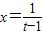
再令g(t)=t-1-lnt,
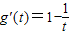 由t∈(1,+∞)知g'(t)>0
由t∈(1,+∞)知g'(t)>0∴当t∈(1,+∞)时,g(t)单调递增∴g(t)>g(1)=0于是t-1>lnt
即
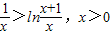 ①
①令
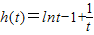 ,
,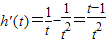 由t∈(1,+∞)知h'(t)>0
由t∈(1,+∞)知h'(t)>0∴当t∈(1,+∞)时,h(t)单调递增∴h(t)>h(1)=0于是
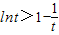
即
 ②
②由①、②可知
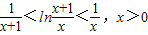 …(10分)
…(10分)所以,
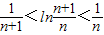 ,即
,即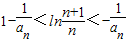 …(11分)
…(11分)(3)由(2)可知
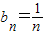 则
则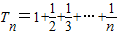
在
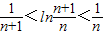 中令n=1,2,3,…,2007,并将各式相加得
中令n=1,2,3,…,2007,并将各式相加得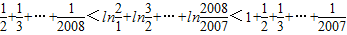
即T2008-1<ln2008<T2007…(14分)
点评:本题以函数为载体,考查新定义,考查函数解析式,考查数列与不等式,有较大的难度.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目