题目内容
如图所示,已知直三棱柱ABC—A1B
证法一:取A1B1中点M,AB中点N,连结AM、B1N、CN、C

∵A
又∵ABC—A1B
∴C
同理可证CN⊥面AA1B1B.
故MA是C
又A1B⊥AC1,∴AM⊥A1B.
又∵AM∥B1N,∴A1B⊥B1N.
而B1N是B
证法二:如图,把直三棱柱补成一个直四棱柱ADBC—A1D1B

∵A
又ADBC—A1D1B
∴A1B1为A1B在底面A1D1B
故A1B⊥D
又∵A1B⊥AC1,∴A1B⊥平面D
故A1B⊥D
∵D
证法三:取A1B1中点M,AB中点N,连结AM、B1N、CN、C
易证平面AMC1∥平面NB
易知C
又A1B⊥AC1,故A1B⊥面AMC1,
且平面AMC1∥平面NB
∴A1B⊥平面NB

练习册系列答案
相关题目
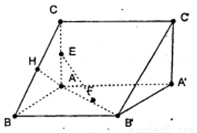
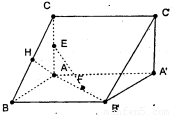
 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,