题目内容
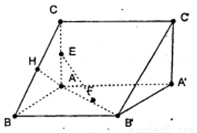
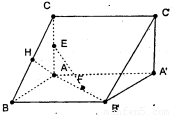
如图所示,已知直三棱柱ABC—A1B1C1中,△ABC为等腰直角三角形,
∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
求证:
(1)DE∥平面ABC;
(2)B1F⊥平面AEF.

证明略
解析:
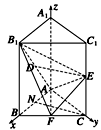
方法一 如图建立空间直角坐标系A—xyz,
令AB=AA1=4,
则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),B1(4,0,4).
(1)取AB中点为N,则N(2,0,0),C(0,4,0),D(2,0,2), 3分
 ∴
∴![]() =(-2,4,0),
=(-2,4,0),![]() =(-2,4,0),
=(-2,4,0),
∴![]() =
=![]() , 4分
, 4分
∴DE∥NC,又NC![]() 平面ABC,DE
平面ABC,DE![]() 平面ABC.
平面ABC.
故DE∥平面ABC. 6分
(2)![]() =(-2,2,-4),
=(-2,2,-4),
![]() =(2,-2,-2),
=(2,-2,-2),![]() =(2,2,0).
=(2,2,0).
![]() ·
·![]() =(-2)×2+2×(-2)+(-4)×(-2)=0,
=(-2)×2+2×(-2)+(-4)×(-2)=0,
则![]() ⊥
⊥![]() ,∴B1F⊥EF, 10分
,∴B1F⊥EF, 10分
∵![]() ·
·![]() =(-2)×2+2×2+(-4)×0=0.
=(-2)×2+2×2+(-4)×0=0.
∴![]() ⊥
⊥![]() ,即B1F⊥AF, 12分
,即B1F⊥AF, 12分
又∵AF∩FE=F,∴B1F⊥平面AEF. 14分
方法二 (1)连接A1B、A1E,并延长A1E交AC的延长线于点P,连接BP.由E为C1C的中点且A1C1∥CP,可证A1E=EP.
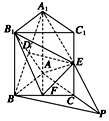 ∵D、E分别是A1B、A1P的中点,
∵D、E分别是A1B、A1P的中点,
所以DE∥BP. 4分
又∵BP![]() 平面ABC,
平面ABC,
DE![]() 平面ABC,
平面ABC,
∴DE∥平面ABC. 6分
(2)∵△ABC为等腰三角形,F为BC的中点,
∴BC⊥AF, 8分
又∵B1B⊥AF,B1B∩BC=B,∴AF⊥平面B1BF,
而B1F![]() 平面B1BF,
平面B1BF,
∴AF⊥B1F. 10分
设AB=A1A=a,
则B1F2=![]() a2,EF2=
a2,EF2=![]() a2,
a2,
B1E2=![]() a2,
a2,
∴B1F2+EF2=B1E2,B1F⊥FE. 12分
又AF∩FE=F,综上知B1F⊥平面AEF. 14分

 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,