Question

（本小题满分12分）

已知椭圆的离心率，连接椭圆的四个顶点得到的菱形的面积为4。

求椭圆的方程；

设直线与椭圆相交于不同的两点，已知点的坐标为（），点在线段的垂直平分线上，且，求的值

Answer 1

【解析】本小题主要考察椭圆的标准方程和几何性质，直线的方程，平面向量等基础知识，考查用代数方法研究圆锥曲线的性质及数形结合的思想，考查运算和推理能力，满分12分

（1）解：由，得，再由，得

由题意可知，

解方程组 得 a=2,b=1

所以椭圆的方程为

(2)解：由（1）可知A（-2,0）。设B点的坐标为（x_1,,y₁）,直线l的斜率为k，则直线l的方程为y=k(x+2),

于是A,B两点的坐标满足方程组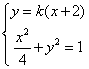

由方程组消去Y并整理，得

由得

设线段AB是中点为M，则M的坐标为

以下分两种情况：

（1）当k=0时，点B的坐标为（2,0）。线段AB的垂直平分线为y轴，于是

（2）当K时，线段AB的垂直平分线方程为

令x=0，解得

由

整理得

综上