题目内容
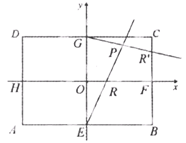
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H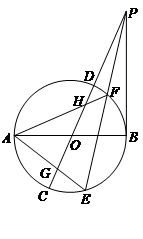
(Ⅰ)设EF中点为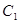 ,求证:O、
,求证:O、 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:利用对角互补得到四点共圆,利用相似得到边长相等.
试题解析:证明:(Ⅰ)
易知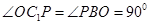 ,
,
所以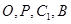 四点共圆. 3分
四点共圆. 3分
(Ⅱ)由(Ⅰ) 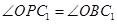
过 作
作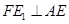 于
于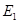 ,交
,交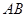 于
于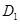
连结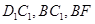
由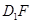 ∥
∥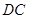 ,
, 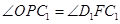
所以
所以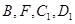 四点共圆. 6分
四点共圆. 6分
所以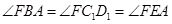 ,由此
,由此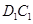 ∥
∥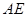 , 8分
, 8分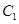 是
是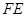 的中点,
的中点,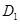 是
是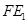 的中点,所以
的中点,所以 ,所以OG ="OH" 10分
,所以OG ="OH" 10分
考点:四点共圆证明;相似证明.

练习册系列答案
相关题目
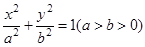 的离心率为
的离心率为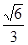 ,且过点
,且过点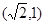 .
.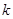 的直线
的直线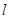 与椭圆相交于不同的两点
与椭圆相交于不同的两点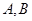 ,试问在
,试问在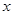 轴上是否存在点
轴上是否存在点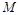 ,使
,使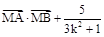 是与
是与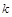 无关的常数?若存在,求出点
无关的常数?若存在,求出点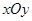 中,已知曲线
中,已知曲线 上任意一点到点
上任意一点到点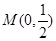 的距离与到直线
的距离与到直线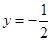 的距离相等.
的距离相等.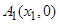 ,
,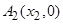 是
是 轴上的两点
轴上的两点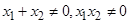 ,过点
,过点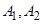 分别作
分别作 ,直线
,直线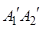 与x轴交于点
与x轴交于点 ,这样就称
,这样就称 确定了
确定了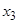 .同样,可由
.同样,可由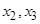 确定了
确定了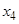 .现已知
.现已知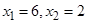 ,求
,求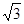 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且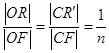 .
.
 :
: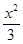 +
+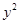 =1上;
=1上;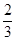 ,求证:直线MN过定点.
,求证:直线MN过定点.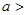
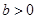 ,曲线
,曲线 上任意一点
上任意一点 分别与点
分别与点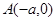 、
、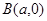 连线的斜率的乘积为
连线的斜率的乘积为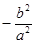 .
.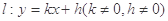 与
与 轴、
轴、 轴分别交于
轴分别交于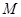 、
、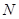 两点,若曲线
两点,若曲线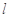 没有公共点,求证:
没有公共点,求证: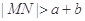 .
.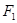 、
、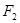 分别是椭圆
分别是椭圆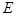 :
: 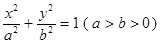 的左、右焦点,点
的左、右焦点,点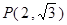 在直线
在直线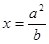 上,线段
上,线段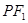 的垂直平分线经过点
的垂直平分线经过点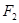 .直线
.直线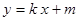 与椭圆
与椭圆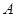 、
、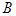 ,且椭圆
,且椭圆 ,使
,使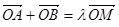 ,其中
,其中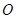 是坐标原点,
是坐标原点,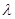 是实数.
是实数.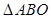 的面积最大?最大面积等于多少?
的面积最大?最大面积等于多少?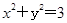 的半径等于椭圆E:
的半径等于椭圆E: (a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-
(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x- 的距离为
的距离为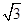 -
-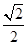 ,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).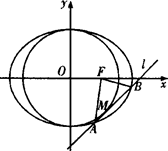
 :
: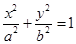
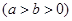 ,称圆心在原点
,称圆心在原点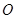 ,半径为
,半径为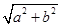 的圆是椭圆
的圆是椭圆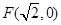 ,且其短轴上的一个端点到
,且其短轴上的一个端点到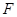 的距离为
的距离为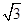 .
.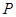 是椭圆
是椭圆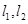 ,使得
,使得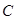 的左右焦点坐标分别是
的左右焦点坐标分别是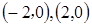 ,离心率
,离心率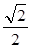 ,直线
,直线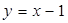 与椭圆
与椭圆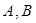 .
.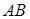 的长度.
的长度.