题目内容
(本小题10分)
已知抛物线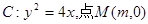 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线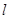 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。
(I)若m=1,且直线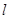 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(II)问是否存在定点M,不论直线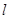 绕点M如何转动,使得
绕点M如何转动,使得 恒为定值。
恒为定值。

【答案】
(I)
(II)存在定点M(2,0)
【解析】 2(I)设A,B两点坐标为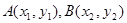 ,AB中点P的坐标为
,AB中点P的坐标为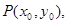
由题意得M(1,0),直线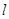 的方程为
的方程为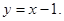
由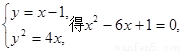
则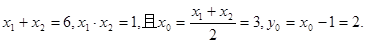
故圆心为P(3,2),直径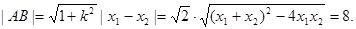
∴以AB为直径的圆的方程为
(II)若存在这样的点M,使得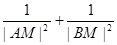 为定值,直线
为定值,直线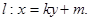
由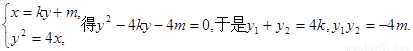
又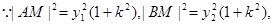
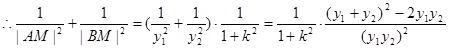
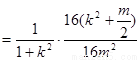 , 13分
, 13分
因为要与k无关,只需令 即m=2,进而
即m=2,进而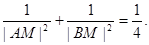
所以,存在定点M(2,0),不论直线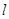 绕点M如何转动,
绕点M如何转动,
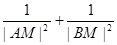 恒为定值
恒为定值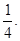

练习册系列答案
相关题目
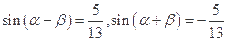 ,且
,且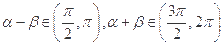 ,求
,求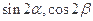 值.
值.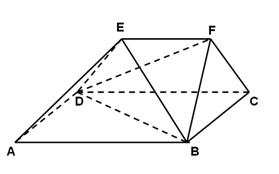
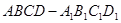 中,
中,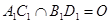 .
.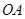 与
与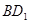 所成角的余弦值;
所成角的余弦值;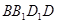 所成角的余弦值.
所成角的余弦值.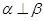 ,
,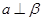 ,
,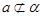 ;求证:
;求证: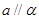 .
.
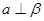 ,
,