题目内容
已知 是定义在
是定义在 上的函数,
上的函数, ,且
,且
 ,总有
,总有
 恒成立.
恒成立.
(Ⅰ)求证: 是奇函数;
是奇函数;
(Ⅱ)对
 ,有
,有 ,
, ,求:
,求:
 及
及 ;
;
(Ⅲ)求
 的最小值.
的最小值.
【答案】
.解:⑴证明: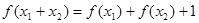 ,
,
令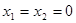 得
得 ,…………………………………2分
,…………………………………2分
再令 ,得
,得
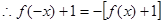 ,函数
,函数 是奇函数.……………………4分
是奇函数.……………………4分
⑵令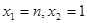 得
得 ,所以
,所以 ,
,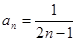 ,
,
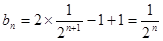 ,
,
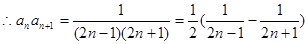
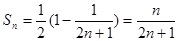 …………………………………..8分
…………………………………..8分
又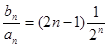 ,
,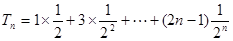 ①
①
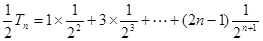 ②
②
由①-②得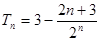 …………………………………………10分
…………………………………………10分
⑶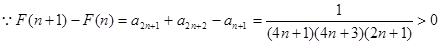
 .
.
又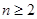 ,
,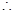
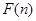 的最小值为
的最小值为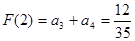 ……………………13分
……………………13分
【解析】略

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 是定义在
是定义在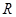 上的函数,
上的函数,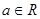 ,那么“对任意的
,那么“对任意的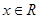 ,
,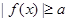 恒成立”的充要条件是( )
恒成立”的充要条件是( )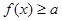 或
或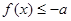 恒成立
恒成立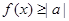 或
或 恒成立
恒成立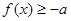 恒成立
恒成立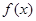 是定义在
是定义在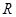 上的函数,且满足
上的函数,且满足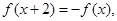 当
当 时,
时, ,则
,则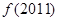 等于 A.
等于 A.
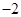 B.2 C.
B.2 C. 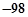 D.
98
D.
98 是定义在
是定义在 上的函数,对任意
上的函数,对任意 都有
都有 ,若函数
,若函数 的图象关于直线
的图象关于直线 对称,且
对称,且 ,则
,则 等于
等于