题目内容
已知函数f(x)=![]() x2-2x,g(x)=logax.如果函数h(x)=f(x)+g(x)没有极值点,且
x2-2x,g(x)=logax.如果函数h(x)=f(x)+g(x)没有极值点,且![]() (x)存在零点.
(x)存在零点.
(1)求a的值;
(2)判断方程f(x)+2=g(x)根的个数并说明理由;
(3)设点A(x1,y1),B(x2,y2)(x1<x2)是函数y=g(x)图象上的两点,平行于AB的切线以P(x0,y0)为切点,求证:x1<x0<x2.
答案:
解析:
解析:
|
解:(1)依题意 所以,所求的a的值为e.5分 (2)方程 设 即函数 由于看不出当 只有通过特殊值来估:当 实际上, 则 则 则方程 (3)由已知: 设 当 所以 同理可得 |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
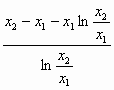
 g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围. x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0. ax2+3x.
ax2+3x.