题目内容
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x) g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
【答案】
(1) 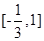 (2)
[1,+∞)
(2)
[1,+∞)
【解析】
试题分析:(1)∵|x+1|≥2|x|?x2+2x+1≥4x2?-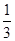 ≤x≤1,
≤x≤1,
∴不等式f(x)≥g(x)的解集为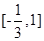 .
.
(2)若任意x∈R, |x+1|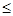 2|x|+a恒成立,即任意x∈R, |x+1|-2|x|
2|x|+a恒成立,即任意x∈R, |x+1|-2|x|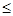 a恒成立,
a恒成立,
令φ(x)=|x+1|-2|x|,则a 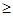 φ(x)max,
φ(x)max,
又φ(x)=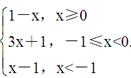
当x≥0时,φ(x)≤1;当-1≤x<0时,-2 ≤φ(x)<1;当x<-1时,φ(x)<-2.
综上可得:φ(x)≤1,
∴a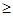 1,即实数a的取值范围为[1,+∞).
1,即实数a的取值范围为[1,+∞).
考点:带绝对值的函数;函数的最值及其几何意义;函数恒成立问题.
点评:本题主要考查绝对值不等式的解法,求函数的最小值,函数的恒成立问题,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有