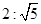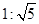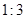题目内容
已知抛物线x2=2py(p>0)的焦点F恰好是双曲线 (a>0,b>0)的一个焦点,且两条曲线交点的连线过点F,则该双曲线的离心率为( )
(a>0,b>0)的一个焦点,且两条曲线交点的连线过点F,则该双曲线的离心率为( )
A. | B.1± | C.1+ | D.无法确定 |
C
解析

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
抛物线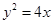 的焦点坐标为( )
的焦点坐标为( )
A.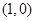 | B.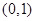 | C.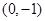 | D.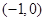 |
已知双曲线的离心率为 ,焦点是
,焦点是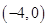 ,
,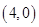 ,则双曲线方程为( )
,则双曲线方程为( )
A.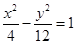 | B.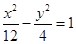 |
C. | D.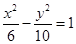 |
[2013·北京高考]双曲线x2- =1的离心率大于
=1的离心率大于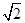 的充分必要条件是( )
的充分必要条件是( )
A.m>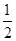 | B.m≥1 | C.m>1 | D.m>2 |
已知点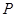 是以
是以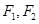 为焦点的双曲线
为焦点的双曲线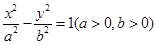 上一点,
上一点,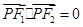 ,
,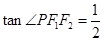 则双曲线的离心率为( )
则双曲线的离心率为( )
A.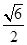 | B.2 | C.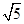 | D.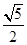 |
已知双曲线 的渐近线方程为
的渐近线方程为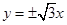 ,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
A.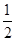 | B.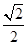 | C.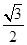 | D.1 |
已知(4,2)是直线l被椭圆 所截得的线段的中点,则l的方程是( )
所截得的线段的中点,则l的方程是( )
| A.x+2y+8=0 |
| B.x+2y-8=0 |
| C.x-2y-8=0 |
| D.x-2y+8=0 |
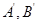 ,则
,则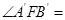 ( )
( ) B.
B.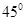 C.
C.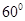 D.
D.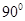
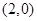 ,抛物线C:
,抛物线C: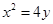 的焦点F。射线FA与抛物线C相交于点M,与其准线相交于点N,则
的焦点F。射线FA与抛物线C相交于点M,与其准线相交于点N,则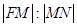 =( )
=( )