题目内容
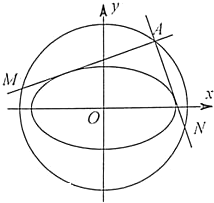 (2013•绍兴一模)已知A是圆x2+y2=4上的一个动点,过点A作两条直线l1,l2,它们与椭圆
(2013•绍兴一模)已知A是圆x2+y2=4上的一个动点,过点A作两条直线l1,l2,它们与椭圆| x2 | 3 |
(1)若A(-2,0),求直线l1,l2的方程;
(2)①求证:对于圆上的任意点A,都有l1⊥l2成立;
②求△AMN面积的取值范围.
分析:(1)设直线方程代入椭圆方程,利用直线与椭圆
+y2=1都只有一个公共点,求出直线的斜率,即可直线l1,l2的方程;
(2)①分类讨论,利用直线斜率的关系,即可证得结论;
②记原点到直线l1,l2的距离分别为d1,d2,表示出△AMN面积,从而可求其取值范围.
| x2 |
| 3 |
(2)①分类讨论,利用直线斜率的关系,即可证得结论;
②记原点到直线l1,l2的距离分别为d1,d2,表示出△AMN面积,从而可求其取值范围.
解答:(1)解:设直线的方程为y=k(x+2),代入椭圆
+y2=1,消去y,可得(1+3k2)x2+12k2x+12k2-3=0
由△=0,可得k2-1=0
设l1,l2的斜率分别为k1,k2,∴k1=-1,k2=1
∴直线l1,l2的方程分别为y=-x-2,y=x+2;
(2)①证明:当直线l1,l2的斜率有一条不存在时,不妨设l1无斜率
∵l1与椭圆只有一个公共点,所以其方程为x=±
当l1的方程为x=
时,此时l1与圆的交点坐标为(
,±1),所以l2的方程为y=1(或y=-1),l1⊥l2成立,
同理可证,当l1的方程为x=-
时,结论成立;
当直线l1,l2的斜率都存在时,设点A(m,n),且m2+n2=4
设方程为y=k(x-m)+n,代入椭圆方程,可得(1+3k2)x2+6k(n-km)x+3(n-km)2-3=0
由△=0化简整理得(3-m2)k2+2mnk+1-n2=0
∵m2+n2=4
∴(3-m2)k2+2mnk+m2-3=0
设l1,l2的斜率分别为k1,k2,∴k1k2=-1,∴l1⊥l2成立
综上,对于圆上的任意点A,都有l1⊥l2成立;
②记原点到直线l1,l2的距离分别为d1,d2,
∵d12+d22=4,∴△AMN面积S2=4d12d22=4d12(4-d12)=-4(d12-2)2+16
∵d12∈[1,3],∴S2∈[12,16]
∴S∈[2
,4].
| x2 |
| 3 |
由△=0,可得k2-1=0
设l1,l2的斜率分别为k1,k2,∴k1=-1,k2=1
∴直线l1,l2的方程分别为y=-x-2,y=x+2;
(2)①证明:当直线l1,l2的斜率有一条不存在时,不妨设l1无斜率
∵l1与椭圆只有一个公共点,所以其方程为x=±
| 3 |
当l1的方程为x=
| 3 |
| 3 |
同理可证,当l1的方程为x=-
| 3 |
当直线l1,l2的斜率都存在时,设点A(m,n),且m2+n2=4
设方程为y=k(x-m)+n,代入椭圆方程,可得(1+3k2)x2+6k(n-km)x+3(n-km)2-3=0
由△=0化简整理得(3-m2)k2+2mnk+1-n2=0
∵m2+n2=4
∴(3-m2)k2+2mnk+m2-3=0
设l1,l2的斜率分别为k1,k2,∴k1k2=-1,∴l1⊥l2成立
综上,对于圆上的任意点A,都有l1⊥l2成立;
②记原点到直线l1,l2的距离分别为d1,d2,
∵d12+d22=4,∴△AMN面积S2=4d12d22=4d12(4-d12)=-4(d12-2)2+16
∵d12∈[1,3],∴S2∈[12,16]
∴S∈[2
| 3 |
点评:本题考查直线与椭圆的位置关系,考查直线方程,考查三角形面积的计算,考查学生分析解决问题的能力,综合性强,难度大.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 (2013•绍兴一模)如图,在△ABC中,
(2013•绍兴一模)如图,在△ABC中,