题目内容
设函数
常数且a∈（0，1）．（1）当a=
时，求f（f（
））；（2）若x满足f（f（x））=x，但f（x）≠x，则称x为f（x）的二阶周期点，试确定函数有且仅有两个二阶周期点，并求二阶周期点x1，x2；
（3）对于（2）中x1，x2，设A（x1，f（f（x1））），B（x2，f（f（x2））），C（a2，0），记△ABC的面积为s（a），求s（a）在区间[
，
]上的最大值和最小值．
【答案】分析：（1）当a=
时，根据所给的函数解析式直接求值即可得出答案；
（2）根据二阶周期点的定义，分段进行求解，找出符号定义的根即为所求；
（3）由题意，先表示出s（a）的表达式，再借助导数工具研究s（a）在区间[
，
]上的单调性，确定出最值，即可求解出最值．
解答：解：（1）当a=
时，求f（
）=
，故f（f（
））=f（
）=2（1-
）=
（2）f（f（x））=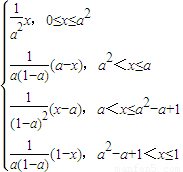
当0≤x≤a2时，由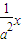
=x，解得x=0，因为f（0）=0，故x=0不是函数的二阶周期点；
当a2＜x≤a时，由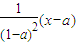
=x，解得x=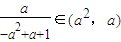
因为f（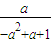
）=
=
≠
，
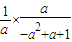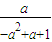故x=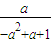
是函数的二阶周期点；
当a＜x≤a2-a+1时，由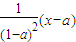
=x，解得x=
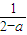∈（a，a2-a+1），因为f（
）=
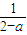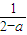，故得x=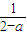
不是函数的二阶周期点；
当a2-a+1＜x≤1时，由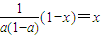
，解得x=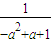
∈（a2-a+1，1），因为f（
）=
≠
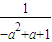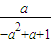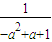，故x=
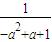是函数的二阶周期点；
因此函数有两个二阶周期点，x1=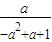
，x2=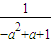
（3）由（2）得A（
，
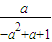），B（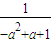
，
）
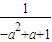则s（a）=S△OCB-S△OCA=
×
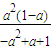，所以s′（a）=
×
，
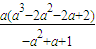因为a∈（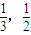
），有a2+a＜1，所以s′（a）=
×
=
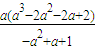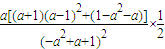＞0（或令g（a）=a3-2a2-2a+2利用导数证明其符号为正亦可）
s（a）在区间[
，
]上是增函数，
故s（a）在区间[
，
]上的最小值为s（
）=
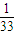，最大值为s（
）=
点评：本题考查求函数的值，新定义的理解，利用导数求函数在闭区间上的最值，第二题解答的关键是理解定义，第三题的关键是熟练掌握导数工具判断函数的单调性，本题考查了方程的思想，转化化归的思想及符号运算的能力，难度较大，综合性强，解答时要严谨认真方可避免会而作不对现象的出现．
时，根据所给的函数解析式直接求值即可得出答案；（2）根据二阶周期点的定义，分段进行求解，找出符号定义的根即为所求；
（3）由题意，先表示出s（a）的表达式，再借助导数工具研究s（a）在区间[
，]上的单调性，确定出最值，即可求解出最值．解答：解：（1）当a=
时，求f（）=，故f（f（））=f（）=2（1-）=（2）f（f（x））=
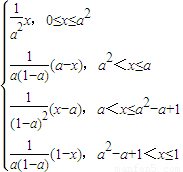
当0≤x≤a2时，由
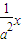=x，解得x=0，因为f（0）=0，故x=0不是函数的二阶周期点；当a2＜x≤a时，由
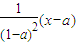=x，解得x=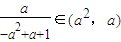因为f（
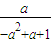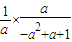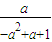）==≠，故x=
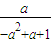是函数的二阶周期点；当a＜x≤a2-a+1时，由
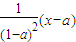=x，解得x=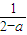∈（a，a2-a+1），因为f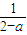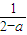（）=，故得x=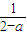不是函数的二阶周期点；当a2-a+1＜x≤1时，由
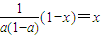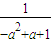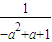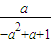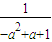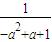，解得x=∈（a2-a+1，1），因为f（）=≠，故x=是函数的二阶周期点；因此函数有两个二阶周期点，x1=
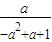，x2=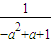（3）由（2）得A（
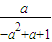，），B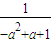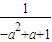（，）则s（a）=S△OCB-S△OCA=
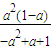×，所以s′（a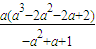）=×，因为a∈（
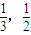），有a2+a＜1，所以s′（a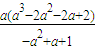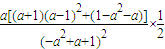）=×=＞0（或令g（a）=a3-2a2-2a+2利用导数证明其符号为正亦可）s（a）在区间[
，]上是增函数，故s（a）在区间[
，]上的最小值为s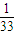（）=，最大值为s（）=点评：本题考查求函数的值，新定义的理解，利用导数求函数在闭区间上的最值，第二题解答的关键是理解定义，第三题的关键是熟练掌握导数工具判断函数的单调性，本题考查了方程的思想，转化化归的思想及符号运算的能力，难度较大，综合性强，解答时要严谨认真方可避免会而作不对现象的出现．
练习册系列答案
阅读快车系列答案
相关题目