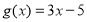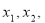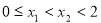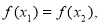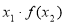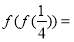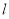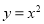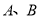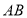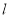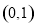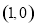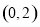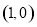题目内容
已知函数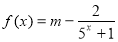
(1)用定义证明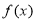 在
在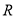 上单调递增;
上单调递增;
(2)若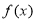 是
是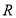 上的奇函数,求
上的奇函数,求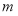 的值;
的值;
(3)若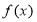 的值域为D,且
的值域为D,且 ,求
,求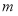 的取值范围.
的取值范围.
(1)设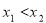 且
且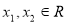
则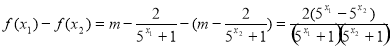
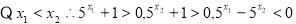
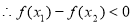 即
即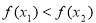
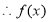 在
在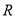 上单调递增 ;
上单调递增 ;
(2)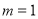 ;(3)
;(3)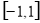 .
.
【解析】
试题分析:(1)在定义域内任取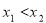 ,证明
,证明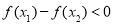 ,即
,即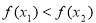 ,所以
,所以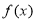 在
在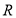 上单调递增;(2)因为,
上单调递增;(2)因为,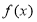 是
是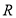 上的奇函数,所以
上的奇函数,所以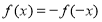 ,即
,即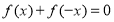 ,代入表达式即可得
,代入表达式即可得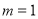 ;(3)可求得
;(3)可求得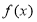 的值域
的值域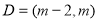 ,由
,由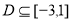 可得不等式
可得不等式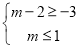 ,所以
,所以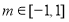 .
.
试题解析:(1)设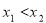 且
且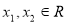 1分
1分
则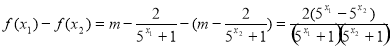 3分
3分
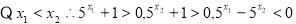
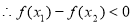 即
即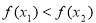 5分
5分
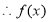 在
在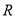 上单调递增 6分
上单调递增 6分
(2)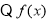 是
是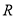 上的奇函数
上的奇函数 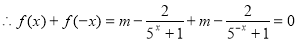 8分
8分
即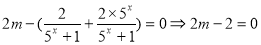
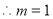 11分
11分
(用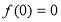 得
得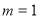 必须检验,不检验扣2分)
必须检验,不检验扣2分)
(3)由
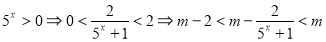
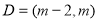 14分
14分
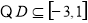
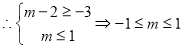
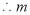 的取值范围是
的取值范围是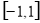 16分
16分
考点:1、函数单调性的证明;2、奇函数的定义;(3)函数的值域.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目