题目内容
求曲线C:xy=1在矩阵A=
|
分析:设P(x0,y0)为曲线xy=1上的任意一点,在矩阵A变换下得到另一点P'(x'0,y'0),根据法则
=
计算A
=
得到P与P′横纵坐标之间的关系,分别用x'0和y'0表示出x0和y0,代入曲线方程即可得到变换后曲线的方程.
|
|
|
|
|
解答:解:设P(x0,y0)为曲线xy=1上的任意一点,在矩阵A变换下得到另一点P'(x'0,y'0),
则有
=
,即
,所以
又因为点P在曲线xy=1上,所以x0y0=1,
故有x'02-y'02=2,即所得曲线方程:x2-y2=2.
则有
|
|
|
|
|
又因为点P在曲线xy=1上,所以x0y0=1,
故有x'02-y'02=2,即所得曲线方程:x2-y2=2.
点评:考查学生掌握二阶矩阵的乘法法则,会求曲线关于矩阵变换后的曲线方程.

练习册系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.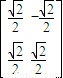 对应的变换作用下得到的曲线C′的方程.
对应的变换作用下得到的曲线C′的方程.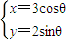 (θ为参数)和曲线C2:ρsin(θ-
(θ为参数)和曲线C2:ρsin(θ-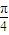 )=
)=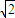 .
.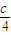 ,|y-b|<
,|y-b|<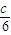 ,求证:|2x-3y-2a+3b|<c.
,求证:|2x-3y-2a+3b|<c.