ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ![]() άΦΆ÷–“ΕΘ§÷–Ιζ ΐ―ßΦ“Φ÷œήΗχ≥ωΝΥ÷±ΒΫΝυ¥ΈΟίΒΡΕΰœν ΫœΒ ΐ±μΘ§»γΆΦΥυ Ψ «ΓΕ―νΜ‘œξΫβΨ≈’¬ΥψΖ®ΓΖΩΣΖΫΉςΖ®±Ψ‘≠Θ§Τδ÷–ΒΎ
άΦΆ÷–“ΕΘ§÷–Ιζ ΐ―ßΦ“Φ÷œήΗχ≥ωΝΥ÷±ΒΫΝυ¥ΈΟίΒΡΕΰœν ΫœΒ ΐ±μΘ§»γΆΦΥυ Ψ «ΓΕ―νΜ‘œξΫβΨ≈’¬ΥψΖ®ΓΖΩΣΖΫΉςΖ®±Ψ‘≠Θ§Τδ÷–ΒΎ![]() ≤ψΦ¥ΈΣ
≤ψΦ¥ΈΣ![]() ’ΙΩΣ ΫΒΡœΒ ΐΘ°Φ÷œή≥Τ’ϊ’≈ ΐ±μΈΣΓΑΩΣΖ≈ΉςΖ®±Ψ‘≠Γ±Θ§Ϋώ≥ΤΓΑΦ÷œή»ΐΫ«Γ±ΒΪΦ÷œήΈ¥Ηχ≥ωΕΰœν ΫœΒ ΐΒΡ“ΜΑψΙΪ ΫΘ§“ρΕχΈ¥ΡήΫ®ΝΔ“ΜΑψ’ΐ’ϊ ΐ¥ΈΟίΒΡΕΰœν ΫΕ®άμΘ°Φ÷œήΒΡ ΐ―ß÷χΉς“― ߥΪΘ§
’ΙΩΣ ΫΒΡœΒ ΐΘ°Φ÷œή≥Τ’ϊ’≈ ΐ±μΈΣΓΑΩΣΖ≈ΉςΖ®±Ψ‘≠Γ±Θ§Ϋώ≥ΤΓΑΦ÷œή»ΐΫ«Γ±ΒΪΦ÷œήΈ¥Ηχ≥ωΕΰœν ΫœΒ ΐΒΡ“ΜΑψΙΪ ΫΘ§“ρΕχΈ¥ΡήΫ®ΝΔ“ΜΑψ’ΐ’ϊ ΐ¥ΈΟίΒΡΕΰœν ΫΕ®άμΘ°Φ÷œήΒΡ ΐ―ß÷χΉς“― ߥΪΘ§![]() άΦΆ ΐ―ßΦ“―νΜ‘‘ΎΓΕœξΫβΨ≈’¬ΥψΖ®ΓΖ
άΦΆ ΐ―ßΦ“―νΜ‘‘ΎΓΕœξΫβΨ≈’¬ΥψΖ®ΓΖ![]() ÷–“ΐ”ΟΝΥΩΣΖ≈ΉςΖ®±Ψ‘≠ΆΦΘ§ΉΔΟς¥ΥΆΦ≥ωΓΑΓΕ ΆΥχΥψ ΐΓΖΘ§Φ÷œή”Ο¥Υ θΓ±Θ§“ρΕχΝς¥Ϊ÷ΝΫώΘ°÷Μ «Κσ»ΥΆυΆυ“ρ¥ΥΑ―ΥϋΈσ≥ΤΈΣΓΑ―νΜ‘»ΐΫ«Γ±Θ°
÷–“ΐ”ΟΝΥΩΣΖ≈ΉςΖ®±Ψ‘≠ΆΦΘ§ΉΔΟς¥ΥΆΦ≥ωΓΑΓΕ ΆΥχΥψ ΐΓΖΘ§Φ÷œή”Ο¥Υ θΓ±Θ§“ρΕχΝς¥Ϊ÷ΝΫώΘ°÷Μ «Κσ»ΥΆυΆυ“ρ¥ΥΑ―ΥϋΈσ≥ΤΈΣΓΑ―νΜ‘»ΐΫ«Γ±Θ°![]() ’ΙΩΣ Ϋ÷–
’ΙΩΣ Ϋ÷–![]() ΒΡœΒ ΐΈΣ
ΒΡœΒ ΐΈΣ![]() Θ§ΔΌ‘ρ Β ΐ
Θ§ΔΌ‘ρ Β ΐ![]() ΒΡ÷ΒΈΣ_______________Θ§ΔΎ’ΙΩΣ Ϋ÷–ΗςœνœΒ ΐ÷°ΚΆΈΣ__________________Θ°
ΒΡ÷ΒΈΣ_______________Θ§ΔΎ’ΙΩΣ Ϋ÷–ΗςœνœΒ ΐ÷°ΚΆΈΣ__________________Θ°

ΓΨ¥πΑΗΓΩ2. 1.
ΓΨΫβΈωΓΩ
ΗυΨίΧβ“βΘ§Ζ÷ΈωΩ…ΒΟ![]() ΘΜ
ΘΜ
Ε‘”ΎΔΌΘΚ”…’ΙΩΣ ΫΩ…ΒΟ![]() Θ§ΫβΩ…ΒΟ
Θ§ΫβΩ…ΒΟ![]() ΒΡ÷ΒΘ§
ΒΡ÷ΒΘ§
Ε‘”ΎΔΎΘ§Νν![]() Ω…ΒΟΘΚ
Ω…ΒΟΘΚ![]() Θ§Φ¥Ω…ΒΟ¥πΑΗΘ°
Θ§Φ¥Ω…ΒΟ¥πΑΗΘ°
ΗυΨίΧβ“βΘΚ![]()
![]() ΘΜ
ΘΜ
Ε‘”ΎΔΌΘ§»τ![]() ’ΙΩΣ Ϋ÷–
’ΙΩΣ Ϋ÷–![]() ΒΡœΒ ΐΈΣ
ΒΡœΒ ΐΈΣ![]() Θ§‘ρ”–
Θ§‘ρ”–![]() Θ§ΫβΩ…ΒΟ
Θ§ΫβΩ…ΒΟ![]() ΘΜ
ΘΜ
Ε‘”ΎΔΎΘ§”…![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
Νν![]() Ω…ΒΟΘΚ
Ω…ΒΟΘΚ![]() Θ§Φ¥’ΙΩΣ Ϋ÷–ΗςœνœΒ ΐ÷°ΚΆΈΣ1ΘΜ
Θ§Φ¥’ΙΩΣ Ϋ÷–ΗςœνœΒ ΐ÷°ΚΆΈΣ1ΘΜ
Ι ¥πΑΗΈΣΘΚΔΌΘ§2ΘΜΔΎΘ§1Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥Τϊ≥ΒΤΖ≈ΤΈΣΝΥΝΥΫβΩΆΜßΕ‘”ΎΤδΤλœ¬ΒΡΈε÷÷–ΆΚ≈Τϊ≥ΒΒΡ¬ζ“β«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥ“Μ–©ΩΆΜßΫχ––ΜΊΖΟΘ§Βς≤ιΫαΙϊ»γœ¬±μΘΚ
Τϊ≥Β–ΆΚ≈ | I | II | III | IV | V |
ΜΊΖΟΩΆΜßΘ®»Υ ΐΘ© | 250 | 100 | 200 | 700 | 350 |
¬ζ“β¬ | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
¬ζ“β¬ «÷ΗΘΚΡ≥÷÷–ΆΚ≈Τϊ≥ΒΒΡΜΊΖΟΩΆΜß÷–Θ§¬ζ“β»Υ ΐ”κΉή»Υ ΐΒΡ±»÷Β.
ΦΌ…ηΩΆΜß «Ζώ¬ζ“βΜΞœύΕάΝΔΘ§«“ΟΩ÷÷–ΆΚ≈Τϊ≥ΒΩΆΜßΕ‘”Ύ¥Υ–ΆΚ≈Τϊ≥Β¬ζ“βΒΡΗ≈¬ ”κ±μΗώ÷–ΗΟ–ΆΚ≈Τϊ≥ΒΒΡ¬ζ“β¬ œύΒ».
(1)¥”Υυ”–ΒΡΜΊΖΟΩΆΜß÷–ΥφΜζ≥ι»Γ1»ΥΘ§«σ’βΗωΩΆΜ߬ζ“βΒΡΗ≈¬ ΘΜ
(2)¥”I–ΆΚ≈ΚΆV–ΆΚ≈Τϊ≥ΒΒΡΥυ”–ΩΆΜß÷–ΗςΥφΜζ≥ι»Γ1»ΥΘ§…ηΤδ÷–¬ζ“βΒΡ»Υ ΐΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘΜ
ΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘΜ
(3)”Ο ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜ߬ζ“βΘ§ ΓΑ
Γ±Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜ߬ζ“βΘ§ ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ± Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜß≤Μ¬ζ“β.–¥≥ωΖΫ≤ν
Γ± Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜß≤Μ¬ζ“β.–¥≥ωΖΫ≤ν![]() ΒΡ¥σ–ΓΙΊœΒ.
ΒΡ¥σ–ΓΙΊœΒ.
ΓΨΧβΡΩΓΩΫϋΡξά¥Θ§ΙζΉ Έ·.Β≥Έ·ΗΏΕ»÷Ί ”ΖωΤΕΩΣΖΔΙΛΉςΘ§ΦαΨωΙα≥Ι¬δ Β÷–―κΖωΤΕΙΛΉς÷Ί¥σΨω≤Ώ≤Ω πΘ§‘ΎΗςΗωΤΕάßœΊ»ΪΝΠΆΤΫχΕ®ΒψΖωΤΕΗςœνΙΛΉςΘ§»ΓΒΟΝΥΜΐΦΪ≥…–ßΘ§Ρ≥ΤΕάßœΊΈΣΝΥœλ”ΠΙζΦ“ΨΪΉΦΖωΤΕΒΡΚ≈’ΌΘ§ΧΊΒΊ≥–ΑϋΝΥ“ΜΩιΆΝΒΊΘ§“―÷ΣΆΝΒΊΒΡ Ι”ΟΟφΜΐ“‘ΦΑœύ”ΠΒΡΙήάμ ±ΦδΒΡΙΊœΒ»γœ¬±μΥυ ΨΘΚ
ΆΝΒΊ Ι”ΟΟφΜΐ | 1 | 2 | 3 | 4 | 5 |
Ιήάμ ±Φδ | 8 | 10 | 13 | 25 | 24 |
≤ΔΒς≤ιΝΥΡ≥¥ε300Οϊ¥εΟώ≤Έ”κΙήάμΒΡ“β‘ΗΘ§ΒΟΒΫΒΡ≤ΩΖ÷ ΐΨί»γœ¬±μΥυ Ψ:
‘Η“β≤Έ”κΙήάμ | ≤Μ‘Η“β≤Έ”κΙήάμ | |
Ρ––‘¥εΟώ | 150 | 50 |
≈°–‘¥εΟώ | 50 |
Θ®1Θ©«σ≥ωœύΙΊœΒ ΐ![]() ΒΡ¥σ–ΓΘ§≤Δ≈–ΕœΙήάμ ±Φδ
ΒΡ¥σ–ΓΘ§≤Δ≈–ΕœΙήάμ ±Φδ![]() ”κΆΝΒΊ Ι”ΟΟφΜΐ
”κΆΝΒΊ Ι”ΟΟφΜΐ![]() «ΖώœΏ–‘œύΙΊΘΩ
«ΖώœΏ–‘œύΙΊΘΩ
Θ®2Θ© «Ζώ”–99.9%ΒΡΑ―Έ’»œΈΣ¥εΟώΒΡ–‘±π”κ≤Έ”κΙήάμΒΡ“β‘ΗΨΏ”–œύΙΊ–‘ΘΩ
Θ®3Θ©»τ“‘ΗΟ¥εΒΡ¥εΟώΒΡ–‘±π”κ≤Έ”κΙήάμ“β‘ΗΒΡ«ιΩωΙάΦΤΤΕάßœΊΒΡ«ιΩωΘ§‘ρ¥”ΗΟΤΕάßœΊ÷–»Έ»Γ3»ΥΘ§Φ«»ΓΒΫ≤Μ‘Η“β≤Έ”κΙήάμΒΡΡ––‘¥εΟώΒΡ»Υ ΐΈΣ![]() ,«σ
,«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΓΘ
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΓΘ
≤ΈΩΦΙΪ ΫΘΚ
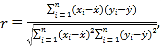
![]()
Τδ÷–![]() ΓΘΝΌΫγ÷Β±μΘΚ
ΓΘΝΌΫγ÷Β±μΘΚ
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
≤ΈΩΦ ΐΨίΘΚ![]()

