题目内容
为了了解某地母亲身高x与女儿身高y的相关关系,现随机测得10对母女的身高,所得数据如下表所示:母亲身高x/cm | 159 | 160 | 160 | 163 | 159 | 154 | 159 | 158 | 159 | 157 |
女儿身高y/cm | 158 | 159 | 160 | 161 | 161 | 155 | 162 | 157 | 162 | 156 |
(1)试对x与y进行一元线性回归分析,并预测当母亲身高为161 cm时,女儿的身高为多少?
(2)求相关系数r,并分析模型的拟合效果.
解析:由题意知先求回归方程,再预测.
解:
i | xi | yi | xi2 | yi2 | xiyi |
1 | 159 | 158 | 25 281 | 24 964 | 25 122 |
2 | 160 | 159 | 25 600 | 25 281 | 25 440 |
3 | 160 | 160 | 25 600 | 25 600 | 25 600 |
4 | 163 | 161 | 26 569 | 25 921 | 26 243 |
5 | 159 | 161 | 25 281 | 25 921 | 25 599 |
6 | 154 | 155 | 23 716 | 24 025 | 23 870 |
7 | 159 | 162 | 25 281 | 26 244 | 25 758 |
8 | 158 | 157 | 24 964 | 24 649 | 24 806 |
9 | 159 | 162 | 25 281 | 26 244 | 25 758 |
10 | 157 | 156 | 24 649 | 24 336 | 24 492 |
∑ | 1 588 | 1 591 | 252 222 | 253 185 | 252 688 |
(1)![]() =
=![]() ,
,![]() =159.1,
=159.1,
b=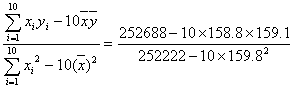
=![]() ≈0.78.
≈0.78.
a=![]() -b
-b![]() =159.1-0.78×158.8=35,
=159.1-0.78×158.8=35,
∴回归方程为y=35+0.78x.
当x=161 cm时,y=160.58 cm,女儿身高为160.58 cm,
(2)r=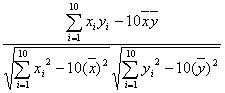
=![]()
=![]() ≈0.715,
≈0.715,
说明用回归方程拟合的较好.
绿色通道
了解相关性检验的必要性.如果不作相关性检验,我们仍然可以求出x与y的回归直线方程.但这时的回归直线方程已经没有任何实际价值了,它也就不能反映变量x与y之间的变化规律.只有在x与y之间具有相关关系时,求回归直线方程才有实际意义,也才可以用于预测取值的情况.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案母亲身高x/cm | 159 | 160 | 160 | 163 | 159 | 154 | 159 | 158 | 159 | 157 |
女儿身高y/cm | 158 | 159 | 160 | 161 | 161 | 155 | 162 | 157 | 162 | 156 |
(1)试对x与y进行线性回归分析,并预测当母亲身高为161 cm时,女儿的身高为多少?
(2)求相关系数r.
| 母亲身x(cm) | 159 | 160 | 160 | 163 | 159 | 154 | 159 | 158 | 159 | 157 |
| 女儿身Y(cm) | 158 | 159 | 160 | 161 | 161 | 155 | 162 | 157 | 162 | 156 |
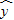 ═34.92+0.78x,因此,当母亲的身高为161cm时,可以估计女儿的身高大致为 .
═34.92+0.78x,因此,当母亲的身高为161cm时,可以估计女儿的身高大致为 . 