题目内容
在平面直角坐标系中,已知A1(-3,0),A2(3,0),P(x,y),M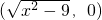 ,O为坐标原点,若实数λ使向量
,O为坐标原点,若实数λ使向量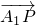 ,
,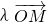 和
和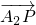 满足:
满足: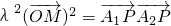 ,设点P的轨迹为W.
,设点P的轨迹为W.
(Ⅰ)求W的方程,并判断W是怎样的曲线;
(Ⅱ)当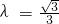 时,过点A1且斜率为1的直线与W相交的另一个交点为B,能否在直线x=-9上找到一点C,恰使△A1BC为正三角形?请说明理由.
时,过点A1且斜率为1的直线与W相交的另一个交点为B,能否在直线x=-9上找到一点C,恰使△A1BC为正三角形?请说明理由.
解:(Ⅰ)由已知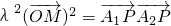 得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1)…(2分)
得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1)…(2分)
①λ2>1,方程为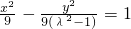 ,焦点在x轴上的双曲线
,焦点在x轴上的双曲线
②λ2=0,圆心在原点,半径为3的圆
③0<λ2<1,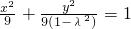 ,焦点在x轴上的椭圆
,焦点在x轴上的椭圆
④λ2=1,直线 y=0…(6分)
(Ⅱ)由(Ⅰ)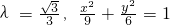
设直线A1B方程为y=x+3,由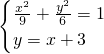 可得5x2+18x+9=0…(10分)
可得5x2+18x+9=0…(10分)
∴A1(-3,0),B(-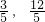 )
)
∴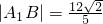 ,
,
在直线x=-9上,离A1(-3,0),最短距离为6,
∴|A1C|> ,故无法形成正三角形
,故无法形成正三角形
∴在直线x=-9上不存在点C,恰使△A1BC为正三角形 …(12分)
分析:(Ⅰ)由已知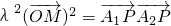 得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1),对λ2分类讨论,即可得到结论;
得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1),对λ2分类讨论,即可得到结论;
(Ⅱ)由(Ⅰ)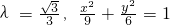 ,由
,由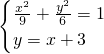 可得5x2+18x+9=0,求得
可得5x2+18x+9=0,求得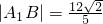 ,|A1C|>
,|A1C|> ,即可得到结论.
,即可得到结论.
点评:本题考查曲线与方程,考查分类讨论的数学思想,考查直线与椭圆的位置关系,属于中档题.
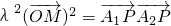 得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1)…(2分)
得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1)…(2分)①λ2>1,方程为
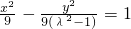 ,焦点在x轴上的双曲线
,焦点在x轴上的双曲线②λ2=0,圆心在原点,半径为3的圆
③0<λ2<1,
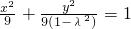 ,焦点在x轴上的椭圆
,焦点在x轴上的椭圆④λ2=1,直线 y=0…(6分)
(Ⅱ)由(Ⅰ)
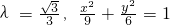
设直线A1B方程为y=x+3,由
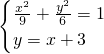 可得5x2+18x+9=0…(10分)
可得5x2+18x+9=0…(10分)∴A1(-3,0),B(-
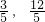 )
)∴
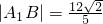 ,
,在直线x=-9上,离A1(-3,0),最短距离为6,
∴|A1C|>
 ,故无法形成正三角形
,故无法形成正三角形∴在直线x=-9上不存在点C,恰使△A1BC为正三角形 …(12分)
分析:(Ⅰ)由已知
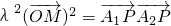 得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1),对λ2分类讨论,即可得到结论;
得λ2(x2-9)=x2-9+y2,即(λ2-1)x2-y2=9(λ2-1),对λ2分类讨论,即可得到结论;(Ⅱ)由(Ⅰ)
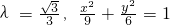 ,由
,由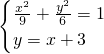 可得5x2+18x+9=0,求得
可得5x2+18x+9=0,求得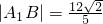 ,|A1C|>
,|A1C|> ,即可得到结论.
,即可得到结论.点评:本题考查曲线与方程,考查分类讨论的数学思想,考查直线与椭圆的位置关系,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目