Question

已知抛物线x²=2py上点（2，2）处的切线经过椭圆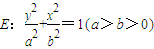的两个顶点．
（1）求椭圆E的方程；
（2）过椭圆E的上顶点A的两条斜率之积为-4的直线与该椭圆交于B、C两点．请问：是否存在一点D，使得直线BC恒过该点？若存在，请求出定点D的坐标；若不存在，请说明理由；
（3）在（2）的条件下，过点A作直线BC的垂线，垂足为H，求点H的轨迹方程．

Answer 1

【答案】分析：（1）利用导数求出抛物线在点（2，2）处的切线方程，得到椭圆的两个顶点坐标，则椭圆方程可求；
（2）设出过A点的两条直线的斜率，写出两条直线AB和AC的直线方程，和椭圆方程联立后求出B和C两点的坐标，结合斜率之积等于-4可以证明直线BC所在的直线方程为，从而说明直线BC过定点（0，0）；
（3）设出H的坐标，由题意可知，代入坐标后可得H的轨迹方程．
解答：解：（1）将（2，2）代入x²=2py，得4=4p，所以p=1，故抛物线方程为x²=2y．
即．
y对x求导得y^′=x，所以抛物线x²=2y上点（2，2）处的切线的斜率为y^′|_x=2=2．
所以抛物线在点（2，2）处的切线方程为y-2=2（x-2），即y=2x-2．
它与两坐标轴的交点分别为（1，0），（0，-2）．
由题意可知，a=2，b=1．
所以椭圆E的方程分别为；
（2）假设直线BC恒过定点D．
设直线AB的斜率k_AB=k₁，直线AC的斜率k_AC=k₂，则k₁k₂=-4．
从而直线AB的方程为y=k₁x+2．
联立，整理得．
从而点B的横坐标，．
所以点B的坐标为．
同理点C的坐标为．
于是，，．
，．
所以点B，C均在直线上．
而两点确定一条直线，所以直线BC的方程为，即．
所以BC恒过定点D（0，0）；
（3）设H（x，y），由（2）知，∠AHO=90°，
所以．
又因为，
所以有x²+y（y-2）=0，即x²+（y-1）²=1．
所以H的轨迹方程为x²+（y-1）²=1（去掉点（0，2））．
点评：本题考查了椭圆的标准方程，考查了利用平面向量求轨迹方程，考查了直线与圆锥曲线的关系，考查了学生灵活处理问题和解决问题的能力，考查了学生的运算能力，属难题．