Question

已知抛物线x²＝2py(p＞0)，过动点M(0，a)，且斜率为1的直线L与该抛物线交于不同两点A、B，|AB|≤2p，

(1)求a的取值范围；

(2)若p＝2，a＝3，求直线L与抛物线所围成的区域的面积；

Answer 1

答案：
解析：

　　解：(1)设直线L方程为：y＝x＋a与抛物线联立方程组得

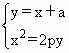
　　x－2px－2ap＝0

　　∴＝4p＋8ap＞0　　a＞－

　　x＋x＝2p　　　x×x＝－2ap

　　＝＝

　　＝

　　解得a≤－

　　∴－＜a≤－

　　(2)若p＝2，a＝3，则直线L方程为：y＝x＋3抛物线方程为x＝4y

　　x－4x－12＝0　　　　∴方程两根为－2和6

　　∴直线与抛物线所围成区域的面积为：

　　S＝＝x＋3x－＝