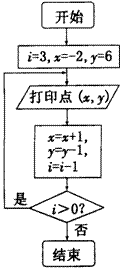
题目内容
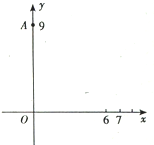在如图所示的直角坐标系中，一运动物体经过点A（0，9），其轨迹方程为y=ax2+c（a＜0），区间D：（6，7）为x轴上的给定区间，为使此物落在区间D内，a的取值范围是-
＜a＜-
| 1 |
| 4 |
| 9 |
| 49 |
-
＜a＜-
．| 1 |
| 4 |
| 9 |
| 49 |
分析：先确定c的值，再利用零点存在定理，建立不等式组，即可得出结论．
解答：解：∵一运动物体经过点A（0，9），其轨迹方程为y=ax2+c（a＜0），
∴c=9
∴f（x）=y=ax2+9
∵（6，7）为x轴上的给定区间，此物落在区间D内，
∴f（6）＞0，f（7）＜0
∴
∴-
＜a＜-
故答案为：-
＜a＜-
∴c=9
∴f（x）=y=ax2+9
∵（6，7）为x轴上的给定区间，此物落在区间D内，
∴f（6）＞0，f（7）＜0
∴
|
∴-
| 1 |
| 4 |
| 9 |
| 49 |
故答案为：-
| 1 |
| 4 |
| 9 |
| 49 |
点评：本题考查零点存在定理，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
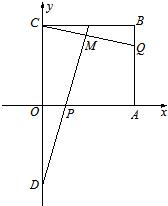如图所示，在直角坐标平面上的矩形OABC中，|OA|=2，
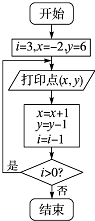利用如图所示程序框图在直角坐标平面上打印一系列点，则打印的点落在坐标轴上的个数是（ ）
本题A、B、C三个选答题，请考生任选一题作答，如果多做，则按所做的第一题计分．
（2012•大丰市一模）如图所示，在直角坐标平面内，反比例函数的图象经过A（1，4），B（a，b），其中a＞1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连接AD、DC、CB．