Question

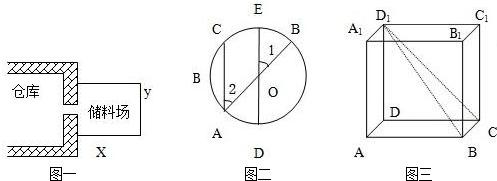
棱长为a的正方体中，连接相邻面的中心，以这些线段为棱的几何体的体积是

 

．

Answer 1

分析：说明几何体的形状，求出底面边长，求出上下两个四棱锥的体积和即可．

解答：解：这是两个底面为正方形的四棱锥对接而成的图形．
每个四棱锥的底面边长与棱长都相等，长度是

2 a

2

所以高度就是

1

2

a
所以每个体积就是（

2 a

2

）²•

a

2

•

1

3

=

a3

12

两个的体积就是：

a3

6

点评：本题考查棱锥的体积，考查正方体的内接体问题，考查计算能力，是基础题．