题目内容
棱长为a的正方体中,连接相邻面的中心,以这些线段为棱的八面体的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:画出图形,根据题意求出八面体的中间平面面积,然后求出其体积.
解答: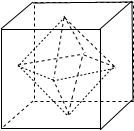 解:画出图就可以了,这个八面体是有两个四棱锥底面合在一起组成的.
解:画出图就可以了,这个八面体是有两个四棱锥底面合在一起组成的.
一个四棱锥的底面面积是正方体的一个面的一半,就是
a2,高为
a,
所以八面体的体积为:2×
×
a2×
a=
.
故选C.
 解:画出图就可以了,这个八面体是有两个四棱锥底面合在一起组成的.
解:画出图就可以了,这个八面体是有两个四棱锥底面合在一起组成的.一个四棱锥的底面面积是正方体的一个面的一半,就是
| 1 |
| 2 |
| 1 |
| 2 |
所以八面体的体积为:2×
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| a3 |
| 6 |
故选C.
点评:本题考查学生空间想象能力,逻辑思维能力,体积的计算公式,考查转化思想,是基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
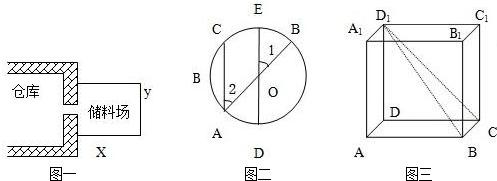
 中,M是AB的中点,则点C到平面
中,M是AB的中点,则点C到平面 的距离为( )
的距离为( )
 B.
B. C.
C. D.
D.