题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:设z=x+yi(x,y∈R,且y≠0),则…………1分 (2x+5)2+(2y)2=(x+10)2+y2. 得到x2+y2=25. ∴|z|=5.……………………2分 |
(2) |
解:∵ = ∴ ∴ 解得m=±5………………7分 |
(3) |
解:(1-2i)z=(1-2i)(x+yi)=(x+2y)+(y-2z)i 依题意,得x+2y=y-2x ∴y=-3x①…………9分 又∵|z|=5,即x2+y2=25②…………10分 由①、②得 ∴z= |

练习册系列答案
相关题目
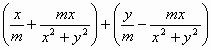 i为实数.…………5分
i为实数.…………5分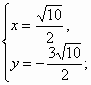 或
或