题目内容

已知点P(x，y)满足
x+y≤4
y≥x
x≥1
，过点P的直线与圆x2+y2=14相交于A，B两点，则|AB|的最小值为（　　）
A、2
B、2
6
C、2
5
D、4
分析：本题主要考查线性规划的基本知识，先画出约束条件
x+y≤4
y≥x
x≥1
的可行域，再求出可行域中各角点的坐标，将各点坐标代入目标函数的解析式，分析后易得直线过在（1，3）处取得最小值．
解答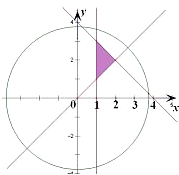：精英家教网解：约束条件
x+y≤4
y≥x
x≥1
的可行域如下图示：
由图易得直线过在（1，3）处取得最小值
最小值为过该点与过该点直径垂直的直线
最小值为4
故选：D
点评：在解决线性规划的小题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域?②求出可行域各个角点的坐标?③将坐标逐一代入目标函数?④验证，求出最优解．
练习册系列答案
相关题目
已知点P在抛物线y=
1
4
x2上，若点P到x轴的距离与点P到抛物线焦点F的距离之比为
1
3
，则点P到焦点F的距离是（　　）
A、
1
2
B、
3
32
C、
1
32
D、
3
2
已知点P在曲线y=
1
3
x3-x+
2
3
上移动，若经过点P的曲线的切线的倾斜角为α，则α的取值范围是
 
．
已知点P是曲线C：
x=2
3
cosθ
y=2sinθ
（θ为参数）上一点，且在第一象限，OP（O是平面直角坐标系的原点）的倾斜角为
π
6
，则点P的坐标为（　　）
A、（
6
，
2
）
B、（
3
，1）
C、（
2
，
6
）
D、（1，
3
）
（2011•惠州模拟）已知点P是圆F1：(x+1)2+y2=8上任意一点，点F2与点F1关于原点对称．线段PF2的中垂线m分别与PF1、PF2交于M、N两点．
（1）求点M的轨迹C的方程；
（2）斜率为k的直线l与曲线C交于P，Q两点，若
OP
•
OQ
=0（O为坐标原点），试求直线l在y轴上截距的取值范围．
已知点P在曲线y=
1
3
x3-x+
2
3
上移动，若经过点P的曲线的切线的倾斜角为α，则α的取值范围是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网