题目内容
函数y=Asin(ωx+∅)(A>0,ω>0,|∅|<π)的图象上有两个相邻的最高点P(
,5)和最低点Q(-
,-5).求
(Ⅰ)此函数的解析式;
(Ⅱ)说明此函数的图象可由y=sinx的图象经过怎样的变换得到?
| π |
| 4 |
| π |
| 12 |
(Ⅰ)此函数的解析式;
(Ⅱ)说明此函数的图象可由y=sinx的图象经过怎样的变换得到?
分析:(I)由函数的最值,得到A=5.根据两个相邻最值点的距离,得到周期T=
,利用周期公式算出ω=3.再根据x=
时函数有最大值5建立关于∅的等式,解出∅=-
即可得到所求函数的解析式;
(II)根据三角函数图象平移、伸缩的公式,结合函数的表达式加以计算,即可得出由y=sinx的图象到所求函数的图象所需经过的变换.
| 2π |
| 3 |
| π |
| 4 |
| π |
| 4 |
(II)根据三角函数图象平移、伸缩的公式,结合函数的表达式加以计算,即可得出由y=sinx的图象到所求函数的图象所需经过的变换.
解答:解:(I)∵图象上有两个相邻的最高点P(
,5)和最低点Q(-
,-5).
∴振幅A=5,函数的周期T=2[
-(-
)]=
,
可得
═
,解之得ω=3.
可得函数表达式为y=5sin(3x+∅).
∵当x=
时,函数有最大值5,
∴5=5sin(3•
+∅),得sin(
+∅)=1,
可得
+∅=
+2kπ(k∈Z),结合|∅|<π,取k=0得∅=-
.
∴此函数的解析式为y=5sin(3x-
);
(2)由三角函数的变换公式,将y=sinx的图象向右平移
单位,得到y=sin(x-
)的图象;
再将所得图象上点的纵坐标不变,横坐标缩短为原来的
倍,得到y=sin(3x-
)的图象;
最后将所得图象上点的横坐标不变,纵坐标伸长为原来的5倍,得到y=5sin(3x-
)的图象.
∴函数y=5sin(3x-
)的图象,可由y=sinx的图象先向右平移
单位,再将所得图象上点的纵坐标不变且横坐标缩短为原来的
倍,最后将所得图象上点的横坐标不变且纵坐标伸长为原来的5倍而得到.
| π |
| 4 |
| π |
| 12 |
∴振幅A=5,函数的周期T=2[
| π |
| 4 |
| π |
| 12 |
| 2π |
| 3 |
可得
| 2π |
| ω |
| 2π |
| 3 |
可得函数表达式为y=5sin(3x+∅).
∵当x=
| π |
| 4 |
∴5=5sin(3•
| π |
| 4 |
| 3π |
| 4 |
可得
| 3π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∴此函数的解析式为y=5sin(3x-
| π |
| 4 |
(2)由三角函数的变换公式,将y=sinx的图象向右平移
| π |
| 4 |
| π |
| 4 |
再将所得图象上点的纵坐标不变,横坐标缩短为原来的
| 1 |
| 3 |
| π |
| 4 |
最后将所得图象上点的横坐标不变,纵坐标伸长为原来的5倍,得到y=5sin(3x-
| π |
| 4 |
∴函数y=5sin(3x-
| π |
| 4 |
| π |
| 4 |
| 1 |
| 3 |
点评:本题给出正弦型三角函数的图象满足的条件,求它的解析式.着重考查了三角函数的周期公式、三角函数的图象的变换与解析式的求法等知识,属于中档题.

练习册系列答案
相关题目
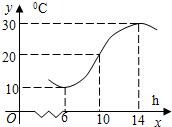 如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若