题目内容
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若|
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若|| OP |
| 10 |
| OP |
| OA |
y=sin(
x-
)
| π |
| 4 |
| π |
| 4 |
y=sin(
x-
)
.| π |
| 4 |
| π |
| 4 |
分析:设P(x0,A),依题意利用向量的数量积的坐标运算通过解方程可求得x0与A的值,继而可求得其周期T,从而可求得ω与φ.
解答:解:设P(x0,A)(A>0),则
=(x0,A),
∵|
|=
,
∴
2=x02+A2=10,①
又
•
=15,A点坐标为(5,0),
∴5x0+0×A=15,
∴x0=3;
将x0=3代入①得A=1.设其周期为T,
∵
=5-3=2,
∴T=8,令ω>0,又T=
,
∴
=8,
∴ω=
.
又函数y=sin(
x+φ)过A(5,0),且在[3,5]上单调递减,
∴
×5+φ=2kπ+π,k∈Z,
令k=0,得φ=-
.
∴y=sin(
x-
).
故答案为:y=sin(
x-
).
| OA |
∵|
| OP |
| 10 |
∴
| OP |
又
| OP |
| OA |
∴5x0+0×A=15,
∴x0=3;
将x0=3代入①得A=1.设其周期为T,
∵
| T |
| 4 |
∴T=8,令ω>0,又T=
| 2π |
| ω |
∴
| 2π |
| ω |
∴ω=
| π |
| 4 |
又函数y=sin(
| π |
| 4 |
∴
| π |
| 4 |
令k=0,得φ=-
| π |
| 4 |
∴y=sin(
| π |
| 4 |
| π |
| 4 |
故答案为:y=sin(
| π |
| 4 |
| π |
| 4 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查向量的数量积与方程思想,求得x0与A的值是关键,也是难点,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•渭南二模)如图,是函数y=Asin(ωx+?),(ω>0,-π<?<π)的图象的一段,O是坐标原点,P是图象的最高点,M点坐标为(5,0),若
(2013•渭南二模)如图,是函数y=Asin(ωx+?),(ω>0,-π<?<π)的图象的一段,O是坐标原点,P是图象的最高点,M点坐标为(5,0),若 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若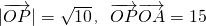 ,则此函数的解析式为________.
,则此函数的解析式为________. ,则此函数的解析式为 .
,则此函数的解析式为 .
 ,则此函数的解析式为 .
,则此函数的解析式为 .