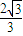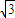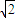题目内容
设双曲线 的右准线与两条渐近线交于A、B两点,右焦点为F,且
的右准线与两条渐近线交于A、B两点,右焦点为F,且 ,那么双曲线的离心率为 .
,那么双曲线的离心率为 .
【答案】分析:先求出A、B两点及右焦点F的坐标,由 及c2=a2+b2,找出a、c的关系,从而求出离心率.
及c2=a2+b2,找出a、c的关系,从而求出离心率.
解答:解:∵双曲线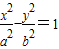 的右准线与两条渐近线交于A、B两点,右焦点为F,
的右准线与两条渐近线交于A、B两点,右焦点为F,
∴A(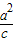 ,
, )、B(
)、B( ,-
,- ),F(c,0),
),F(c,0),
∵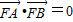 ,∴(
,∴( -c,
-c, )•(
)•(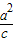 -c,-
-c,- )=0,
)=0,
又c2=a2+b2,∴ =
=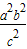 ,∴
,∴ =
= ,
,
c2=2a2,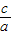 =
= ;
;
故答案为 .
.
点评:本题考查双曲线的几何性质及2个向量的数量积运算.
 及c2=a2+b2,找出a、c的关系,从而求出离心率.
及c2=a2+b2,找出a、c的关系,从而求出离心率.解答:解:∵双曲线
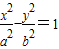 的右准线与两条渐近线交于A、B两点,右焦点为F,
的右准线与两条渐近线交于A、B两点,右焦点为F,∴A(
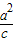 ,
, )、B(
)、B( ,-
,- ),F(c,0),
),F(c,0),∵
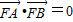 ,∴(
,∴( -c,
-c, )•(
)•(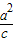 -c,-
-c,- )=0,
)=0,又c2=a2+b2,∴
 =
=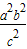 ,∴
,∴ =
= ,
,c2=2a2,
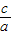 =
= ;
;故答案为
 .
.点评:本题考查双曲线的几何性质及2个向量的数量积运算.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 的右准线与两条渐近线交于A、B两点,右焦点为F,且
的右准线与两条渐近线交于A、B两点,右焦点为F,且 ,那么双曲线的离心率为 .
,那么双曲线的离心率为 .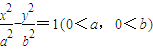 的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )
的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )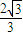
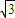
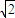
 的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )
的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )