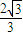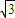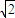题目内容
设双曲线 的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )
的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )A.
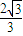
B.2
C.
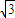
D.
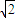
【答案】分析:关键是条件“以AB为直径的圆经过点F”如何用,故先计算FC的长,再计算AB的长,利用|AB|=2|FC|,建立双曲线特征值a、b、c间的等式,解方程即可得双曲线的离心率
解答:解:依题意设AB的中点为C,则C( ,0),F(c,0),∴|FC|=c-
,0),F(c,0),∴|FC|=c- =
=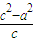 =
=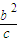
将x= 代入双曲线渐近线方程y=
代入双曲线渐近线方程y= x,得y=
x,得y= =
=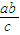 ,∴|AB|=
,∴|AB|=
∵以AB为直径的圆经过点F,∴|AB|=2|FC|
∴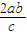 =
=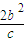 ,即a2=b2,即c2=2a2
,即a2=b2,即c2=2a2
∴双曲线的离心率为e=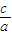 =
=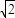
故选D
点评:本题考察了双曲线的标准方程和几何性质离心率的求法,解题时要熟练的将几何条件进行转化,具有一定的代数变换能力
解答:解:依题意设AB的中点为C,则C(
 ,0),F(c,0),∴|FC|=c-
,0),F(c,0),∴|FC|=c- =
=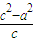 =
=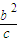
将x=
 代入双曲线渐近线方程y=
代入双曲线渐近线方程y= x,得y=
x,得y= =
=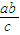 ,∴|AB|=
,∴|AB|=
∵以AB为直径的圆经过点F,∴|AB|=2|FC|
∴
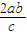 =
=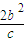 ,即a2=b2,即c2=2a2
,即a2=b2,即c2=2a2∴双曲线的离心率为e=
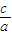 =
=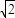
故选D
点评:本题考察了双曲线的标准方程和几何性质离心率的求法,解题时要熟练的将几何条件进行转化,具有一定的代数变换能力

练习册系列答案
相关题目
 的右准线与两条渐近线交于A、B两点,右焦点为F,且
的右准线与两条渐近线交于A、B两点,右焦点为F,且 ,那么双曲线的离心率为 .
,那么双曲线的离心率为 . 的右准线与两条渐近线交于A、B两点,右焦点为F,且
的右准线与两条渐近线交于A、B两点,右焦点为F,且 ,那么双曲线的离心率为 .
,那么双曲线的离心率为 .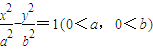 的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )
的右准线与两渐近交于A,B两点,点F为右焦点,若以AB为直径的圆经过点F,则该双曲线的离心率为( )