题目内容
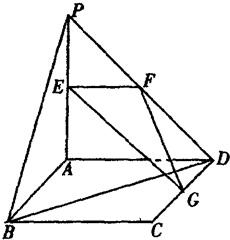 如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(1)求证:面EFG⊥面PAB;
(2)求异面直线EG与BD所成的角;
(3)求点A到面EFG的距离.
分析:解法一(1)由已知中ABCD为正方形,△PAD是直角三角形,可得AD⊥AB,AD⊥PA,进而由线面垂直的判定定理得到AD⊥面PAB,结合E、F分别是线段PA、PD的中点及三角形中位线定理可得EF/AD,结合线面垂直的第二判定定理可得EF⊥面PAB,再由面面垂直的判定定理得到面EFG⊥面PAB;
(2)取BC的中点M,连接GM、AM、EM,由异面直线夹角的定义可得∠EGM(或其补角)就是异面直线EG与BD所成的角,解△MAE可得答案.
(3)取AB中点H,连接GH,HE,过点A作AT⊥HE于T,则AT就是点A到平面EFG的距离,解Rt△AEH,即可得到点A到面EFG的距离.
解法二:(1)以A为原点建立如图所示的空间直角坐标系A-xyz,分别求出向量
,
,
的坐标,根据两个向量数量积为0,向量垂直,易判断出EF⊥AP,EF⊥AB,结合线面垂直的判定定理得到答案.
(2)分别求出向量
,
的方向向量,代入向量夹角公式,即可得到答案.
(3)求出平面EFC的法向量
,及向量
的坐标,代入点A到平面EFG的距离公式d=|
|,可得答案.
(2)取BC的中点M,连接GM、AM、EM,由异面直线夹角的定义可得∠EGM(或其补角)就是异面直线EG与BD所成的角,解△MAE可得答案.
(3)取AB中点H,连接GH,HE,过点A作AT⊥HE于T,则AT就是点A到平面EFG的距离,解Rt△AEH,即可得到点A到面EFG的距离.
解法二:(1)以A为原点建立如图所示的空间直角坐标系A-xyz,分别求出向量
| EF |
| AP |
| AB |
(2)分别求出向量
| EG |
| BD |
(3)求出平面EFC的法向量
| n |
| AE |
| ||||
|
|
解答:解法一(1)证明:∵ABCD为正方形,△PAD是直角三角形,
且PA=AD=2,∴AD⊥AB,AD⊥PA
又AB∩PA=A,∴AD⊥面PAB.…(1分)
∵E、F分别是线段PA、PD的中点,
∴EF/AD,∴EF⊥面PAB.…(2分)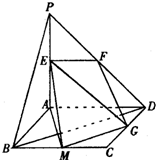
又EF?面EFG,∴面EFG⊥面PAB.…(3分)
(2)解:取BC的中点M,连接GM、AM、EM,则GM∥BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.(4分)
在Rt△MAE中,EM=
=
,
同理EG=
,…(5分)
又GM=
BD=
,∴在△MGE中,cos∠EGM=
=
=
…(6分)
故异面直线EG与BD所成的角为arccos
,…(7分)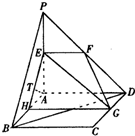
(3)解:取AB中点H,连接GH,HE,则GH∥AD∥EF,
∴E、F、G、H四点共面,过点A作AT⊥HE于T,
∵面EFGH⊥面PAB,∴AT⊥平面EFGH,…(9分)
∴AT就是点A到平面EFG的距离.…(10分)
在Rt△AEH中,AE=AH=1,
∴AT=
=
=
,
故点A到平面EFG的距离为
.…(12分)
解法二:建立如图所示的空间直角坐标系A-xyz,
 则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
(1)证明:∵
=(0,1,0),
=(0,0,2),
=(2,0,0),
∴
•
=0×0+1×0+0×2=0,
•
=0×2+1×0+0×0=0,
∴EF⊥AP,EF⊥AB.…(1分)
又∵AP、AB?面PAB,且PA∩AB=A,
∴EF⊥平面PAB.…(2分)
又EF?面EFG,∴平面EFG⊥平面PAB.…(3分)
(2)解:∵
=(1,2,-1),
=(-2,2,0),…(4分)
∴cos<
,
>=
=
=
,…(6分)
故异面直线EG与BD所成的角为arcos
.…(7分)
(3)解:设平面EFC的法向量
=(x,y,z),…(8分)
则
∴
…(10分)
令z=0,得
=(1,0,1).…(11分)
又
=(0,0,1),∴点A到平面EFG的距离d=|
|=|
|=
.…(12分)
且PA=AD=2,∴AD⊥AB,AD⊥PA
又AB∩PA=A,∴AD⊥面PAB.…(1分)
∵E、F分别是线段PA、PD的中点,
∴EF/AD,∴EF⊥面PAB.…(2分)

又EF?面EFG,∴面EFG⊥面PAB.…(3分)
(2)解:取BC的中点M,连接GM、AM、EM,则GM∥BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.(4分)
在Rt△MAE中,EM=
| EA2+AM2 |
| 6 |
同理EG=
| 6 |
又GM=
| 1 |
| 2 |
| 2 |
| EG2+GM2-ME2 |
| 2EG•GM |
| 6+2-6 | ||||
2
|
| ||
| 6 |
故异面直线EG与BD所成的角为arccos
| ||
| 6 |

(3)解:取AB中点H,连接GH,HE,则GH∥AD∥EF,
∴E、F、G、H四点共面,过点A作AT⊥HE于T,
∵面EFGH⊥面PAB,∴AT⊥平面EFGH,…(9分)
∴AT就是点A到平面EFG的距离.…(10分)
在Rt△AEH中,AE=AH=1,
∴AT=
| AE•AH |
| EH |
| 1×1 | ||
|
| ||
| 2 |
故点A到平面EFG的距离为
| ||
| 2 |
解法二:建立如图所示的空间直角坐标系A-xyz,
 则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).
(1)证明:∵
| EF |
| AP |
| AB |
∴
| EF |
| AP |
| EF |
| AB |
∴EF⊥AP,EF⊥AB.…(1分)
又∵AP、AB?面PAB,且PA∩AB=A,
∴EF⊥平面PAB.…(2分)
又EF?面EFG,∴平面EFG⊥平面PAB.…(3分)
(2)解:∵
| EG |
| BD |
∴cos<
| EG |
| BD |
| ||||
|
|
| -2+4 | ||||
|
| ||
| 6 |
故异面直线EG与BD所成的角为arcos
| ||
| 6 |
(3)解:设平面EFC的法向量
| n |
则
|
|
令z=0,得
| n |
又
| AE |
| ||||
|
|
| 1 | ||
|
| ||
| 2 |
点评:本题考查的知识点是向量语言表述直线的垂直关系,点到平面的距离运算,用空间向量求直线间的夹角,其中解法一(几何法)的关键是熟练掌握空间线面关系的判定、性质及相互转换;解法二(向量法)的关键是建立恰当的空间坐标系,将空间线面关系问题转化为向量夹角问题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.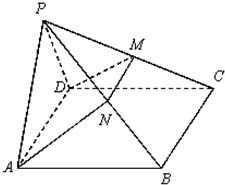 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.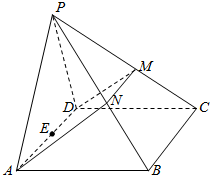 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.