题目内容
设0≤x≤2π,且 ,则x的取值范围是 .
,则x的取值范围是 .
【答案】分析:将已知等式左边被开方数利用同角三角函数间的基本关系变形后,利用完全平方公式化简,再利用二次根式的化简公式变形,得到sinx大于cosx,由x的范围,利用正弦及余弦函数图象即可得出x的范围.
解答:解:∵ =
= =
=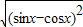 =|sinx-cosx|=sinx-cosx,
=|sinx-cosx|=sinx-cosx,
∴sinx-cosx≥0,即sinx≥cosx,
∵0≤x≤2π,
∴x的取值范围是 ≤x≤
≤x≤ .
.
故答案为: ≤x≤
≤x≤
点评:此题考查了同角三角函数间的基本关系,完全平方公式的运用,二次根式的化简公式,以及正弦、余弦函数的图象与性质,将已知等式进行适当的变形是解本题的关键.
解答:解:∵
 =
= =
=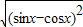 =|sinx-cosx|=sinx-cosx,
=|sinx-cosx|=sinx-cosx,∴sinx-cosx≥0,即sinx≥cosx,
∵0≤x≤2π,
∴x的取值范围是
 ≤x≤
≤x≤ .
.故答案为:
 ≤x≤
≤x≤
点评:此题考查了同角三角函数间的基本关系,完全平方公式的运用,二次根式的化简公式,以及正弦、余弦函数的图象与性质,将已知等式进行适当的变形是解本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目