题目内容
设0≤x≤2π,且
=sinx-cosx,则x的取值范围是
| 1-2sinx.cosx |
[
,
]
| π |
| 4 |
| 5π |
| 4 |
[
,
]
.| π |
| 4 |
| 5π |
| 4 |
分析:根据题意可得sin x≥cosx,因此同一坐标系内作出y=sin x和y=cosx的图象,找出它们的交点A、B的坐标,结合图象即可得到满足条件的x的取值范围.
解答:解:∵
=|cosx-sin x|=sinx-cosx,
∴sinx-cosx≥0,可得sin x≥cosx
同一坐标系内作出y=sin x和y=cosx的图象
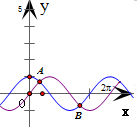
∵y=sin x和y=cosx的图象交于点A(
,
)和B(
,-
)
∴当sin x≥cosx成立时,x的取值范围为[
,
]
故答案为:[
,
]
| 1-2sinx.cosx |
∴sinx-cosx≥0,可得sin x≥cosx
同一坐标系内作出y=sin x和y=cosx的图象

∵y=sin x和y=cosx的图象交于点A(
| π |
| 4 |
| ||
| 2 |
| 5π |
| 4 |
| ||
| 2 |
∴当sin x≥cosx成立时,x的取值范围为[
| π |
| 4 |
| 5π |
| 4 |
故答案为:[
| π |
| 4 |
| 5π |
| 4 |
点评:本题给出三角函数的等式,要我们求x的取值范围,着重考查了三角函数的符号和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目