题目内容
【题目】已知二次函数![]() 的导函数的图像与直线
的导函数的图像与直线![]() 平行,且
平行,且![]() 在
在![]() 处取得极小值
处取得极小值![]() .设
.设![]() .
.
(1)若曲线![]() 上的点
上的点![]() 到点
到点![]() 的距离的最小值为
的距离的最小值为![]() ,求
,求![]() 的值;
的值;
(2)![]() 如何取值时,函数
如何取值时,函数![]() 存在零点,并求出零点.
存在零点,并求出零点.
【答案】(1)![]() ;(2)当k=1时,有一个零点
;(2)当k=1时,有一个零点![]() ;当
;当
![]() 时,有一个零点
时,有一个零点![]() ;当
;当![]() 或
或![]() 时,函数有两个零点
时,函数有两个零点![]() .
.
【解析】试题分析:(1)先根据二次函数的顶点式设出函数![]() 的解析式,然后对其进行求导,根据
的解析式,然后对其进行求导,根据![]() 的导函数的图象与直线
的导函数的图象与直线![]() 平行求出
平行求出![]() 的值,进而可确定函数
的值,进而可确定函数![]() 的解析式,然后设出点
的解析式,然后设出点![]() 的坐标,根据两点间的距离公式表示出
的坐标,根据两点间的距离公式表示出![]() ,再由基本不等式表示其最小值,解方程即可得结果;(2)先根据(1)的内容得到函数
,再由基本不等式表示其最小值,解方程即可得结果;(2)先根据(1)的内容得到函数![]() 的解析式,即
的解析式,即![]() ,然后先对二次项的系数等于0进行讨论,再当二次项的系数不等于0即为二次方程时,根据方程的判别式进行讨论即可得到答案.
,然后先对二次项的系数等于0进行讨论,再当二次项的系数不等于0即为二次方程时,根据方程的判别式进行讨论即可得到答案.
试题解析:(1)依题可设![]() ,则
,则![]() ,又
,又![]() 的图象与直线
的图象与直线![]() 平行,
平行,![]() ,
,![]() ,
,![]() ,设
,设![]() ,则
,则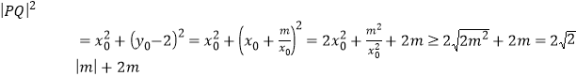 当且仅当
当且仅当![]() 时,
时,![]() 取得最小值,即
取得最小值,即![]() 取得最小值
取得最小值![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() .
.
(2)由![]() ,得
,得![]() ,当
,当![]() 时,方程
时,方程![]() 有一解
有一解![]() ,函数
,函数![]() 有一零点,
有一零点,![]() ;当
;当![]() 时,方程
时,方程![]() 有二解
有二解![]() ,若
,若![]() ,函数
,函数![]() 有两个零点,
有两个零点,![]() ,即
,即![]() ,若
,若![]() ,
,
函数![]() 有两零点,
有两零点,![]() ,即
,即![]()
当![]() 时,方程
时,方程![]() 有一解
有一解![]() ,函数
,函数![]() 有一零点,
有一零点,![]() ,综上,当
,综上,当![]() 时,函数
时,函数![]() 有一零点,
有一零点,![]() ;当
;当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点,
有两个零点,![]() ,当
,当![]() 时,函数
时,函数![]() 有一个零点
有一个零点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y= ![]() 中,
中, 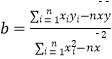 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.