题目内容
已知函数f(x)=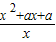 ,且a<1.
,且a<1.(1)当x∈[1,+∞)时,判断f(x)的单调性并证明;
(2)在(1)的条件下,若m满足f(3m)>f(5-2m),试确定m的取值范围.
(3)设函数g(x)=x•f(x)+|x2-1|+(k-a)x-a,k为常数.若关于x的方程g(x)=0在(0,2)上有两个解x1,x2,求k的取值范围,并比较
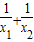 与4的大小.
与4的大小.
【答案】分析:(1)根据函数单调性的定义,首先应在所给区间上任设两个数并规定大小,然后通过作差法分析获得两数对应函数值之间的大小关系即可;
(2)首先要将抽象不等式结合函数的奇偶性进行转化,然后根据函数的单调性找到自变量之间的不等关系,注意定义域优先原则.
(3)首先将函数进行化简,或为分段函数,通过研究两段函数的单调性即可获得两根的分布情况,由根的条件以及根的分布即可获得k的取值范围.最后可以通过消参数的办法:通过两个根对应的方程分别将k用两根表示出;或解方程的思想:直接将两根用变量k表出解答问题.
解答:解:(1)由题得:f(x)=x+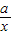 +a,设1≤x1<x2,
+a,设1≤x1<x2,
则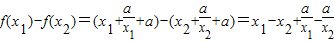
=(x1-x2)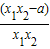 ,
,
∵1≤x1<x2,∴x1-x2<0,x1x2>1,又a<1,得x1x2-a>0
∴f(x1)-f(x2)<0,即f(x)在[1,+∞)上为增函数.
(2)由(1)得:f(x)在[1,+∞)上为增函数,
要满足f(5-2m)<f(3m)
只要1≤5-2m<3m,
∴m的取值范围为:1<m≤2.
(3)g(x)=x•f(x)+|x2-1|+(k-a)x-a=x2+kx+|x2-1|
g(x)=0在(0,2)上有两个解x1,x2,不妨设0<x1<x2<2,
g(x)=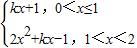 ,
,
所以g(x)在(0,1]是单调函数,
故g(x)=0在(0,1]上至多一个解,
若1<x1<x2<2,则x1x2=- <0,
<0,
故不符题意,
因此0<x1≤1<x2<2.
由g(x1)=0得k=-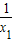 ,所以k≤-1;
,所以k≤-1;
由g(x2)=0得k=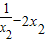 ,所以-
,所以- <k<-1;
<k<-1;
故当- <k<-1时,方程g(x)=0在(0,2)上有两个解.
<k<-1时,方程g(x)=0在(0,2)上有两个解.
方法一:因为0<x1≤1<x2<2,
所以k=-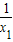 ,2x22+kx2-1=0
,2x22+kx2-1=0
消去k得2x1x22-x1-x2=0
即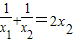 ,因为x2<2,
,因为x2<2,
所以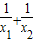 <4.
<4.
方法二:由g(x1)=0得x1=-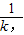
由2x2+kx-1=0得x= ;
;
因为x2∈(1,2),所以x2= .
.
则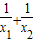 =-k+
=-k+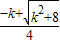 =
=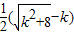 .
.
而y=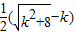 =
=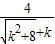 在
在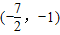 上是减函数,
上是减函数,
则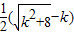 <
<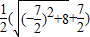 =4.
=4.
因此,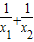 <4.
<4.
点评:本题考查的是函数单调性的综合应用问题.在解答的过程当中充分体现了函数的性质、抽象不等式的解答以及函数与方程的思想和问题转化的能力.
(2)首先要将抽象不等式结合函数的奇偶性进行转化,然后根据函数的单调性找到自变量之间的不等关系,注意定义域优先原则.
(3)首先将函数进行化简,或为分段函数,通过研究两段函数的单调性即可获得两根的分布情况,由根的条件以及根的分布即可获得k的取值范围.最后可以通过消参数的办法:通过两个根对应的方程分别将k用两根表示出;或解方程的思想:直接将两根用变量k表出解答问题.
解答:解:(1)由题得:f(x)=x+
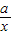 +a,设1≤x1<x2,
+a,设1≤x1<x2,则
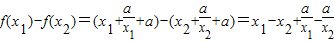
=(x1-x2)
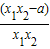 ,
,∵1≤x1<x2,∴x1-x2<0,x1x2>1,又a<1,得x1x2-a>0
∴f(x1)-f(x2)<0,即f(x)在[1,+∞)上为增函数.
(2)由(1)得:f(x)在[1,+∞)上为增函数,
要满足f(5-2m)<f(3m)
只要1≤5-2m<3m,
∴m的取值范围为:1<m≤2.
(3)g(x)=x•f(x)+|x2-1|+(k-a)x-a=x2+kx+|x2-1|
g(x)=0在(0,2)上有两个解x1,x2,不妨设0<x1<x2<2,
g(x)=
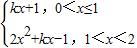 ,
,所以g(x)在(0,1]是单调函数,
故g(x)=0在(0,1]上至多一个解,
若1<x1<x2<2,则x1x2=-
 <0,
<0,故不符题意,
因此0<x1≤1<x2<2.
由g(x1)=0得k=-
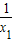 ,所以k≤-1;
,所以k≤-1;由g(x2)=0得k=
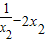 ,所以-
,所以- <k<-1;
<k<-1;故当-
 <k<-1时,方程g(x)=0在(0,2)上有两个解.
<k<-1时,方程g(x)=0在(0,2)上有两个解.方法一:因为0<x1≤1<x2<2,
所以k=-
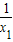 ,2x22+kx2-1=0
,2x22+kx2-1=0消去k得2x1x22-x1-x2=0
即
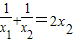 ,因为x2<2,
,因为x2<2,所以
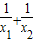 <4.
<4.方法二:由g(x1)=0得x1=-
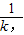
由2x2+kx-1=0得x=
 ;
;因为x2∈(1,2),所以x2=
 .
.则
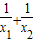 =-k+
=-k+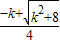 =
=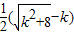 .
.而y=
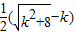 =
=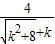 在
在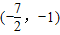 上是减函数,
上是减函数,则
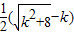 <
<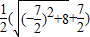 =4.
=4.因此,
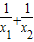 <4.
<4.点评:本题考查的是函数单调性的综合应用问题.在解答的过程当中充分体现了函数的性质、抽象不等式的解答以及函数与方程的思想和问题转化的能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|