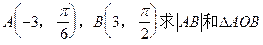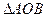题目内容
已知直线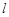 的参数方程为
的参数方程为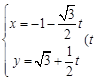 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,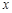 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆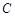 的极坐标方程为
的极坐标方程为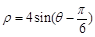 .求:
.求:
(1)求圆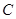 的直角坐标方程;
的直角坐标方程;
(2)若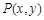 是直线
是直线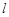 与圆面
与圆面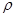 ≤
≤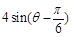 的公共点,求
的公共点,求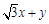 的取值范围.
的取值范围.
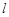 的参数方程为
的参数方程为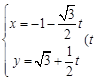 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,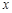 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆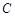 的极坐标方程为
的极坐标方程为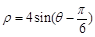 .求:
.求:(1)求圆
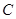 的直角坐标方程;
的直角坐标方程;(2)若
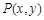 是直线
是直线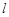 与圆面
与圆面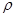 ≤
≤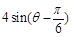 的公共点,求
的公共点,求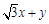 的取值范围.
的取值范围.(1)
 .(2)
.(2) .
.

 .(2)
.(2) .
.试题分析:(1)先将
 利用两角差的正弦公式展开,方程两边在乘以
利用两角差的正弦公式展开,方程两边在乘以 ,利用直角坐标与极坐标互化公式即可将极坐标方程互为直角坐标方程;(2)先将直线方程化为普通方程互化,求出直线与圆的交点A、B坐标,作出直线
,利用直角坐标与极坐标互化公式即可将极坐标方程互为直角坐标方程;(2)先将直线方程化为普通方程互化,求出直线与圆的交点A、B坐标,作出直线 :
: =0,平移直线
=0,平移直线 ,结合图形,找出直线z=
,结合图形,找出直线z= 与线段AB相交时,z取最大值与最小值点,求出z的最大值与最小值,即可求出
与线段AB相交时,z取最大值与最小值点,求出z的最大值与最小值,即可求出 的取值范围.
的取值范围.试题解析:(1)因为圆
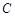 的极坐标方程为
的极坐标方程为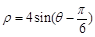
所以

又

所以


所以圆
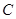 的直角坐标方程为:
的直角坐标方程为:
 . 6分
. 6分(2)『解法1』:
设

由圆
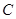 的方程
的方程



所以圆
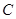 的圆心是
的圆心是 ,半径是
,半径是
将
 代入
代入 得
得
又直线
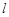 过
过 ,圆
,圆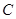 的半径是
的半径是 ,由题意有:
,由题意有:
所以

即
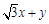 的取值范围是
的取值范围是 . 14分
. 14分『解法2』:
直线
 的参数方程化成普通方程为:
的参数方程化成普通方程为:
由

解得
 ,
,
∵
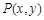 是直线
是直线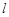 与圆面
与圆面 的公共点,
的公共点,∴点
 在线段
在线段 上,
上,∴
 的最大值是
的最大值是 ,
,最小值是

∴
 的取值范围是
的取值范围是 . 14分
. 14分
练习册系列答案
相关题目
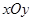 中,直线
中,直线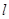 的参数方程为
的参数方程为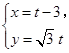 (
(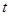 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系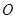 为极点,以
为极点,以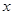 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线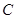 的极坐标方程为
的极坐标方程为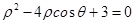 .
.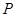 是曲线
是曲线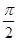 ).若直线l过点P,且倾斜角为
).若直线l过点P,且倾斜角为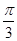 ,圆C以M为圆心, 4为半径.
,圆C以M为圆心, 4为半径.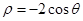 的圆心的极坐标为( )
的圆心的极坐标为( )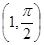


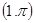
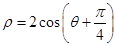 ,则该圆的半径是 .
,则该圆的半径是 .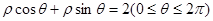 与
与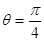 的交点的极坐标是( )
的交点的极坐标是( )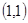
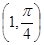

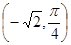
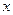 轴正半轴为极轴建立极坐标系,有下列命题:
轴正半轴为极轴建立极坐标系,有下列命题: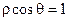 与曲线
与曲线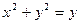 无公共点;
无公共点;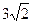 ,
,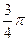 )的点
)的点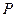 所对应的复数是-3+3i;
所对应的复数是-3+3i;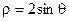 的圆心到直线
的圆心到直线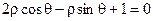 的距离是
的距离是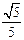 ;
; 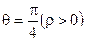 与曲线
与曲线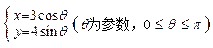 相交于点
相交于点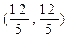 .
.