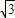题目内容
过抛物线y2=8(x+2)的焦点F作倾斜角为45°的直线交抛物线于A、B两点,且|AF|>|BF|,过点A作与x轴垂直的直线交抛物线于点C,则△BCF的面积是( )A.16
B.8
C.64
D.32
【答案】分析:由题意可得抛物线y2=8(x+2)的焦点F(0,0)即为原点O,所作直线AB的方程为y=x,联立方程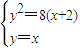 可得x2-8x-16=0,由AF>BF可得从而可求A,B,C 的坐标,进而可求三角形的面积
可得x2-8x-16=0,由AF>BF可得从而可求A,B,C 的坐标,进而可求三角形的面积
解答:解:由题意可得抛物线y2=8(x+2)的焦点F(0,0)即为原点O
∴所作直线AB的方程为y=x
联立方程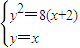 可得x2-8x-16=0
可得x2-8x-16=0
由AF>BF可得xA>xB
∴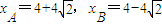 ,
,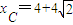
即B(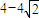 ,4-4
,4-4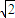 ),C(4+4
),C(4+4 ,-4-4
,-4-4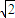 ),A(4+4
),A(4+4 ,4+4
,4+4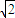 )
)
∴KOC=-1,KOB=1,即OC⊥OB
则S△FBC=S△OBC=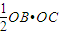 =
=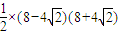 =16
=16
故选A
点评:本题主要考察了抛物线的性质的应用,直线与抛物线的相交关系的应用,还考察了基本运算的能力.
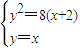 可得x2-8x-16=0,由AF>BF可得从而可求A,B,C 的坐标,进而可求三角形的面积
可得x2-8x-16=0,由AF>BF可得从而可求A,B,C 的坐标,进而可求三角形的面积解答:解:由题意可得抛物线y2=8(x+2)的焦点F(0,0)即为原点O
∴所作直线AB的方程为y=x
联立方程
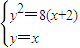 可得x2-8x-16=0
可得x2-8x-16=0由AF>BF可得xA>xB
∴
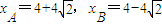 ,
,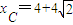
即B(
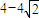 ,4-4
,4-4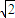 ),C(4+4
),C(4+4 ,-4-4
,-4-4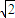 ),A(4+4
),A(4+4 ,4+4
,4+4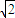 )
)∴KOC=-1,KOB=1,即OC⊥OB
则S△FBC=S△OBC=
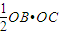 =
=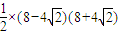 =16
=16故选A
点评:本题主要考察了抛物线的性质的应用,直线与抛物线的相交关系的应用,还考察了基本运算的能力.

练习册系列答案
相关题目