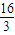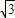题目内容
过抛物线y2=8（x+2）的焦点F作倾斜角为60°的直线，若此直线与抛物线交于A、B两点，弦AB的中垂线与x轴交于点P，则线段PF的长等于（ ）
A．
| B．
| C．
| D．8
|
由抛物线的方程为 y2=8（x+2），可得 p=4，它的焦点F（0，0），
弦AB所在的直线方程为 y=
x，把它代入抛物线方程化简可得3x2-8x-16=0，
故x1+x2=
，故AB的中点为（
，
），故AB的中垂线方程为 y-
=-
（x-
）．
再令y=0，解得x=
，故点P的横坐标为
，即 PF=
．
故选A．
弦AB所在的直线方程为 y=
| 3 |
故x1+x2=
| 8 |
| 3 |
| 4 |
| 3 |
| 4 | ||
|
| 4 | ||
|
| 1 | ||
|
| 4 |
| 3 |
再令y=0，解得x=
| 16 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
故选A．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
