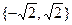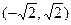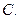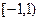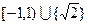题目内容
(本小题共12分)
设函数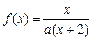 ,方程
,方程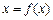 有唯一解,其中实数
有唯一解,其中实数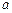 为常数,
为常数,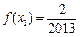 ,
,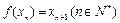
(1)求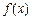 的表达式;
的表达式;
(2)求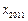 的值;
的值;
(3)若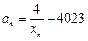 且
且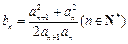 ,求证:
,求证: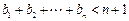
设函数
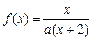 ,方程
,方程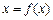 有唯一解,其中实数
有唯一解,其中实数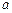 为常数,
为常数,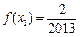 ,
,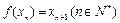
(1)求
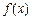 的表达式;
的表达式;(2)求
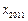 的值;
的值;(3)若
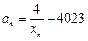 且
且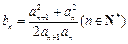 ,求证:
,求证: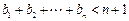
解:(1)由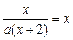 ,可化简为
,可化简为
 -------2分
-------2分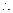 当且仅当
当且仅当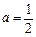 时,方程
时,方程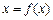 有唯一解. ---3分
有唯一解. ---3分
从而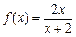 -------4分
-------4分
(2)由已知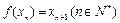 ,得
,得 -------5分
-------5分
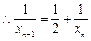 ,即
,即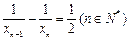
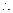 数列
数列
 是
是 以
以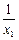 为首项,
为首项,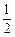 为公差的等差数列. -------6分
为公差的等差数列. -------6分
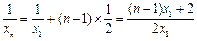 ,
,
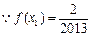 ,
, ,即
,即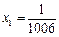
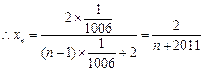 -------7分
-------7分
故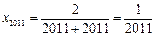 -------8分
-------8分
(3)证明: ,
, -------10分
-------10分
 ---11分
---11分

故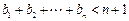
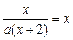 ,可化简为
,可化简为
 -------2分
-------2分 当且仅当
当且仅当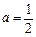 时,方程
时,方程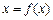 有唯一解. ---3分
有唯一解. ---3分从而
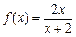 -------4分
-------4分(2)由已知
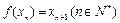 ,得
,得 -------5分
-------5分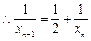 ,即
,即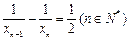
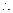 数列
数列
 是
是 以
以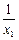 为首项,
为首项,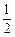 为公差的等差数列. -------6分
为公差的等差数列. -------6分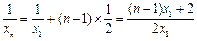 ,
,
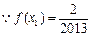 ,
, ,即
,即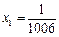
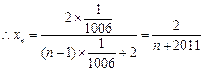 -------7分
-------7分故
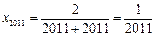 -------8分
-------8分(3)证明:
 ,
, -------10分
-------10分 ---11分
---11分
故
略

练习册系列答案
相关题目
 ,若
,若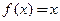 ,则称
,则称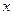 为
为 ,则称
,则称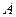 和
和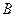 ,即
,即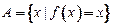 ,
, .
.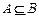 ;
; ,且
,且 ,求实数
,求实数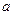 的取值范围;
的取值范围; 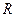 上的单调递增函数,
上的单调递增函数,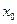 是函数的稳定点,问
是函数的稳定点,问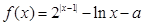 恰有两个不同的零点,则
恰有两个不同的零点,则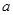 的取值范围是( )
的取值范围是( )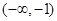
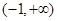
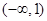
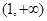

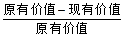 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)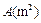 的宿舍楼.已知土地的征用费为2388元/
的宿舍楼.已知土地的征用费为2388元/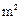 ,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍.经工程技术人员核算,第一.二层的建筑费用都为445元/
,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍.经工程技术人员核算,第一.二层的建筑费用都为445元/ 计这幢宿舍楼的楼高层数,使总费用最小,并求出其最小费用.(总费用为建筑费用和征地费用之和)
计这幢宿舍楼的楼高层数,使总费用最小,并求出其最小费用.(总费用为建筑费用和征地费用之和)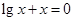 在下列的哪个区间内有实数解( )
在下列的哪个区间内有实数解( )
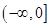
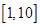
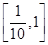
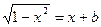 只有一个根,则
只有一个根,则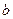 的取值集合为 ( )
的取值集合为 ( )