题目内容
填空题(1)已知
 ,则sin2x的值为______.
,则sin2x的值为______.(2)已知定义在区间
 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______
【答案】分析:(1)利用三角函数的恒等变换化简已知条件可得cos(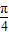 +x)=
+x)= ,由sin2x=-cos(
,由sin2x=-cos(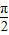 +2x),利用二倍角的余弦公式求出结果.
+2x),利用二倍角的余弦公式求出结果.
(2)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案.
(3)由条件求得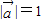 ,
,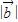 =1,再由得
=1,再由得 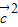 =
=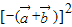 =
=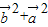 +2
+2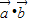 =2,即可求得值.
=2,即可求得值.
解答:解:(1)∵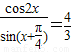 =
=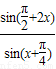 =
=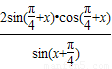 =2cos(
=2cos(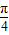 +x),
+x),
∴cos(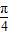 +x)=
+x)= ,∴sin2x=-cos(
,∴sin2x=-cos(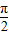 +2x)=-[2
+2x)=-[2 -1]=-(-
-1]=-(- )=
)= ,
,
故答案为 .
.
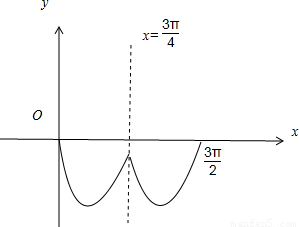
(2)依题意作出函数y=f(x)在区间[0,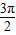 ]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0.
]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0.
①当 <a≤0,f(x)=a有2个解,②当
<a≤0,f(x)=a有2个解,②当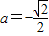 时,f(x)=a有3个解,
时,f(x)=a有3个解,
③当-1<a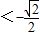 时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,
时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,
故方程f(x)=a有四个不同的解,则实数a的取值范围为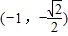 ,
,
故答案为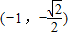 .
.
(3)由题意可得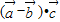 =
=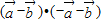 =0,∴
=0,∴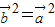 ,
, =
=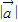 .
.
再由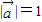 ,可得
,可得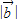 =1.
=1.
再由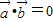 ,
,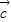 =-(
=-(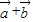 ) 可得
) 可得 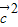 =
=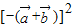 =
=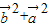 +2
+2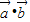 =2.
=2.
∴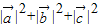 =4,
=4,
故答案为4.
点评:本题主要考查三角函数的恒等变换及化简求值,函数的图象及性质,两个向量的数量积的定义,数量积公式的应用,体现了转化、数形结合、分类讨论的数学思想,属于中档题.
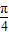 +x)=
+x)= ,由sin2x=-cos(
,由sin2x=-cos(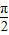 +2x),利用二倍角的余弦公式求出结果.
+2x),利用二倍角的余弦公式求出结果.(2)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案.
(3)由条件求得
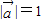 ,
,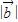 =1,再由得
=1,再由得 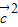 =
=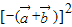 =
=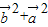 +2
+2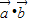 =2,即可求得值.
=2,即可求得值.解答:解:(1)∵
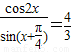 =
=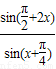 =
=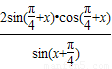 =2cos(
=2cos(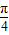 +x),
+x),∴cos(
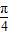 +x)=
+x)= ,∴sin2x=-cos(
,∴sin2x=-cos(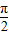 +2x)=-[2
+2x)=-[2 -1]=-(-
-1]=-(- )=
)= ,
,故答案为
 .
.(2)依题意作出函数y=f(x)在区间[0,
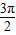 ]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0.
]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0.①当
 <a≤0,f(x)=a有2个解,②当
<a≤0,f(x)=a有2个解,②当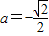 时,f(x)=a有3个解,
时,f(x)=a有3个解,③当-1<a
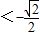 时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,
时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,故方程f(x)=a有四个不同的解,则实数a的取值范围为
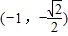 ,
,故答案为
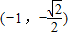 .
.
(3)由题意可得
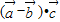 =
=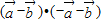 =0,∴
=0,∴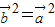 ,
, =
=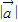 .
.再由
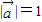 ,可得
,可得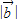 =1.
=1.再由
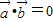 ,
,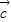 =-(
=-(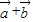 ) 可得
) 可得 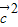 =
=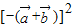 =
=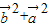 +2
+2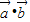 =2.
=2.∴
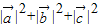 =4,
=4,故答案为4.
点评:本题主要考查三角函数的恒等变换及化简求值,函数的图象及性质,两个向量的数量积的定义,数量积公式的应用,体现了转化、数形结合、分类讨论的数学思想,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
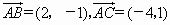 ,则
,则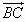 =_____________;
=_____________;
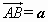 ,
,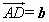 为基底向量,则
为基底向量,则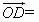 ________;
________;
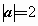 ,
,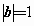 ,且
,且 ,则a与b的夹角为________;
,则a与b的夹角为________;
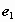
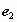 是单位向量,且
是单位向量,且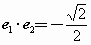 ,则
,则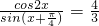 ,则sin2x的值为________.
,则sin2x的值为________.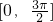 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线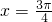 对称,当
对称,当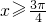 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________.
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________. 满足
满足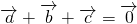 ,
,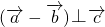 ,
, ,若
,若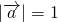 ,则
,则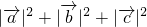 的值是________.
的值是________.