题目内容
设斜率为2的直线过抛物线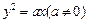 的焦点F,且
的焦点F,且 和y轴交与点A,若
和y轴交与点A,若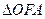 (O为坐标原点)的面积为4,则抛物线的方程为 ( )
(O为坐标原点)的面积为4,则抛物线的方程为 ( )
A. | B.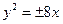 | C.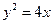  | D.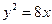 |
略
解析

练习册系列答案
相关题目
已知双曲线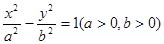 的左右焦点分别 为F1、F2,P是准线上一点,且
的左右焦点分别 为F1、F2,P是准线上一点,且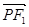 ·
·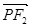 =0,
=0,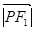 ·
·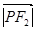 =4ab,则双曲线的离心率是
=4ab,则双曲线的离心率是
A.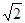 | B.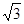 | C.2 | D.3 |
如果椭圆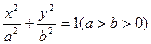 的离心率为
的离心率为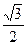 ,那么双曲线
,那么双曲线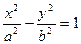 的离心率是 ( )
的离心率是 ( )
A.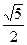 | B. | C.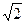 | D.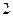 |
以椭圆短轴为直径的圆经过此椭圆的焦点,则椭圆的离心率是( )
A.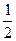 | B.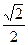 | C.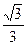 | D.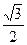 |
已知双曲线的两个焦点为F1(-,0)、F2(,0),M是此双曲线上的一点,且 满足
满足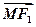 ·
·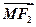 =0,|
=0,|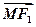 |·|
|·|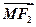 |=2,则该双曲线的方程是( )
|=2,则该双曲线的方程是( )
| A.-y2=1 | B.x2-=1 | C.-=1 | D.-=1 |
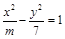 ,直线l过其左焦点F1,交双曲线左支于A、B两点,且|AB|=4,F2为双曲线的右焦点,△ABF2的周长为20,则m的值为 ( )
,直线l过其左焦点F1,交双曲线左支于A、B两点,且|AB|=4,F2为双曲线的右焦点,△ABF2的周长为20,则m的值为 ( )  为正数,
为正数, ,
, 其中
其中 是常数,且
是常数,且 的最小值是
的最小值是 ,满足条件的点
,满足条件的点 是椭圆
是椭圆 一弦的中点,则此弦所在的直线方程为
一弦的中点,则此弦所在的直线方程为



 、
、 、
、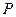 是双曲线
是双曲线 上不同的三点,且
上不同的三点,且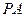 、
、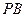 的斜率乘积
的斜率乘积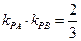 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) 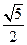 B.
B.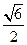 C.
C.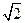 D.
D.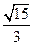
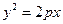 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则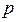 的值为( )
的值为( )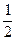 B 1 C 2 D 4
B 1 C 2 D 4