题目内容
已知双曲线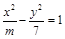 ,直线l过其左焦点F1,交双曲线左支于A、B两点,且|AB|=4,F2为双曲线的右焦点,△ABF2的周长为20,则m的值为 ( )
,直线l过其左焦点F1,交双曲线左支于A、B两点,且|AB|=4,F2为双曲线的右焦点,△ABF2的周长为20,则m的值为 ( )
A.8 B.9 C.16 D.20
B
解析考点:双曲线的简单性质;双曲线的定义.
分析:应用双曲线的定义和△ABF2的周长为20,解出半长轴,可求m的值.
解析:由已知,|AB|+|AF2|+|BF2|=20,又|AB|=4,则|AF2|+|BF2|=16.
据双曲线定义,2a=|AF2|-|AF1|=|BF2|-|BF1|,
所以4a=|AF2|+|BF2|-(|AF1|+|BF1|)=16-4=12,
即a=3,所以m=a2=9,
故选B.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
椭圆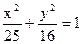 的离心率为 ( )
的离心率为 ( )
A.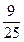  | B.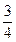 | C.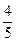 | D.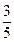 |
我国于2010年10月1日成功发射嫦娥二号卫星,卫星飞行约两小时到达月球,到达月球以后,经过几次变轨将绕月球以椭圆型轨道飞行,其轨迹是以月球的月心为一焦点的椭圆。若第一次变轨前卫星的近月点到月心的距离为m,远月点到月心的距离为n,第二次变轨后两距离分别为2m,2n.则第一次变轨前的椭圆离心率比第二次变轨后的椭圆离心率 ( )
| A.变大 | B.变小 | C.不变 | D.与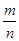 的大小有关 的大小有关 |
抛物线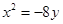 的准线方程为
的准线方程为
| A.x=2 | B.x= 2 2 | C.y=2 | D.y= 2 2 |
抛物线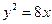 的准线方程是
的准线方程是 ( )
( )
A.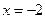 | B.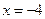 | C.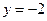 | D.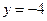 |
已知点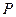 在椭圆
在椭圆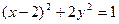 上,则
上,则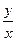 的最大值是( )
的最大值是( )
A.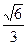 | B.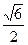 | C.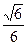 | D.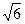 |
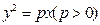 上,则这个正三角形的边长为
上,则这个正三角形的边长为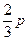
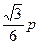
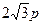
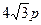
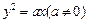 的焦点F,且
的焦点F,且 和y轴交与点A,若
和y轴交与点A,若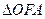 (O为坐标原点)的面积为4,则抛物线的方程为 ( )
(O为坐标原点)的面积为4,则抛物线的方程为 ( )