题目内容
已知双曲线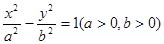 的左右焦点分别 为F1、F2,P是准线上一点,且
的左右焦点分别 为F1、F2,P是准线上一点,且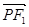 ·
·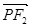 =0,
=0,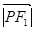 ·
·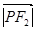 =4ab,则双曲线的离心率是
=4ab,则双曲线的离心率是
A.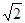 | B.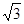 | C.2 | D.3 |
B
解析考点:双曲线的简单性质.
分析:设右准线与x轴的交点为A,根据PF1⊥PF2,利用射影定理可得|PA|2=|AF1|×|AF2|,利用P到x轴的距离为 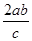 可建立方程,从而求出双曲线的离心率.
可建立方程,从而求出双曲线的离心率.
解:∵P是右准线上一点,P到x轴的距离为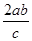
∴可设P(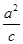 ,
,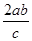 )
)
设右准线与x轴的交点为A,
∵PF1⊥PF2,
∴|PA|2=|AF1|×|AF2|
∴(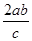 )2=(c+
)2=(c+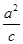 )(c-
)(c-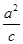 )
)
∴4a2b2=(c2-a2)(c2+a2)
∴4a2=c2+a2
∴3a2=c2
∴e=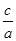 =
=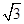
故选B.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
.椭圆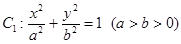 的左准线为
的左准线为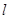 ,左、右焦点分别为
,左、右焦点分别为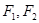 ,抛物线
,抛物线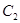 的准线也为
的准线也为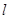 ,焦点为
,焦点为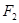 ,记
,记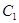 与
与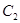 的一个交点为
的一个交点为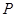 ,则
,则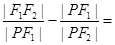 ( )
( )
A.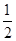 | B.1 | C.2 | D.与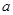 , ,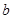 的取值有关 的取值有关 |
若椭圆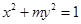 的离心率为
的离心率为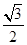 ,则它的长半轴长为( )
,则它的长半轴长为( )
| A.1 | B.2 | C.1或2 | D.与m有关 |
如果双曲线的半实轴长为2,焦距为6,那么该双曲线的离心率是 ( )
A.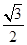 | B.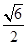 | C.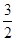 | D.2 |
椭圆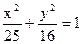 的离心率为 ( )
的离心率为 ( )
A.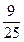  | B.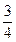 | C.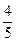 | D.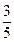 |
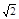
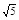
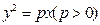 上,则这个正三角形的边长为
上,则这个正三角形的边长为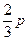
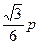
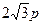
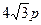
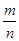 的大小有关
的大小有关 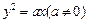 的焦点F,且
的焦点F,且 和y轴交与点A,若
和y轴交与点A,若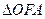 (O为坐标原点)的面积为4,则抛物线的方程为 ( )
(O为坐标原点)的面积为4,则抛物线的方程为 ( )