题目内容
 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.写出y关于x的函数关系式,并指出这个函数的定义域.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.写出y关于x的函数关系式,并指出这个函数的定义域.分析:由于S△AEH=S△CFG=
x2,S△BEF=S△DGH=
(a-x)(2-x)所以y=SABCD-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x,由各边长大于0,可求定义域.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意可知:S△AEH=S△CFG=
x2,S△BEF=S△DGH=
(a-x)(2-x)
∴y=SABCD-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x
由
,解得0<x≤2,
∴y=-2x2+(a+2)x,0<x≤2
定义域为(0,2].
| 1 |
| 2 |
| 1 |
| 2 |
∴y=SABCD-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x
由
|
∴y=-2x2+(a+2)x,0<x≤2
定义域为(0,2].
点评:本题为实际应用问题,由题意构建函数模型是解决问题的关键,属基础题.

练习册系列答案
相关题目
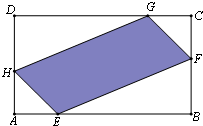 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y. (
( ,绿地面积为
,绿地面积为 .
.
 (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
. (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
.