题目内容
(本小题满分12分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
( 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为 .
.
(1)写出 关于
关于 的函数关系式,指出这个函数的定义域.
的函数关系式,指出这个函数的定义域.
(2)当AE为何值时,绿地面积最大?
【答案】
(1)∴y=-2x2+(a+2)x,0<x≤2
(2)当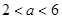 时,AE=
时,AE=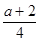 时,绿地面积取最大值
时,绿地面积取最大值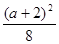 ;
;
当a≥6时,AE=2时,绿地面积取最大值2a-4
【解析】(1)SΔAEH=SΔCFG=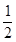 x2,
x2,
SΔBEF=SΔDGH=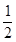 (a-x)(2-x)。
(a-x)(2-x)。
∴y=SABCD-2SΔAEH-2SΔBEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x。
由 ,得
,得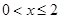
∴y=-2x2+(a+2)x,0<x≤2
(2)当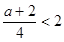 ,即
,即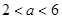 时,则x=
时,则x=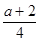 时,y取最大值
时,y取最大值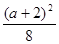
当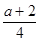 ≥2,即a≥6时,y=-2x2+(a+2)x,在
≥2,即a≥6时,y=-2x2+(a+2)x,在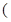 0,2]上是增函数,
0,2]上是增函数,
则x=2时,y取最大值2a-4
综上所述:当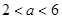 时,AE=
时,AE=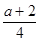 时,绿地面积取最大值
时,绿地面积取最大值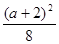 ;
;
当a≥6时,AE=2时,绿地面积取最大值2a-4

练习册系列答案
相关题目