题目内容
已知ABCD为空间四边形，已知 AB=CD，AD=BC，但 AB≠AD，M，N为两对角线的中点，则
- A.MN与AC，BD都垂直
- B.MN仅与AC，BD中之一垂直
- C.MN与AC，BD都不垂直
- D.无法确定MN与AC，BD是否垂直
A
分析：先证明△ABD与△BCD全等，再证△ADM与△CBM全等，从而得到AM=MC，又N点为AC的中点，利用等腰三角形的中线就是高从而MN⊥AC，同理证出MN⊥BD，得到结论．
解答：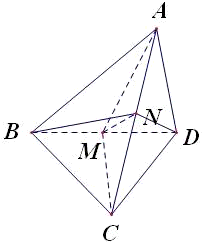
解：
∵AB=CD，AD=BC，BD=BD
∴△ABD≌△BCD，又M点为BD的中点
∴△ADM≌△CBM
∴AM=MC，又N点为AC的中点
∴MN⊥AC，同理可证MN⊥BD
故选A．
点评：本题主要考查了空间中直线与直线之间的位置关系，以及棱锥的结构特征，考查空间想象能力、运算能力和推理论证能力，属于基础题．
分析：先证明△ABD与△BCD全等，再证△ADM与△CBM全等，从而得到AM=MC，又N点为AC的中点，利用等腰三角形的中线就是高从而MN⊥AC，同理证出MN⊥BD，得到结论．
解答：
解：∵AB=CD，AD=BC，BD=BD
∴△ABD≌△BCD，又M点为BD的中点
∴△ADM≌△CBM
∴AM=MC，又N点为AC的中点
∴MN⊥AC，同理可证MN⊥BD
故选A．
点评：本题主要考查了空间中直线与直线之间的位置关系，以及棱锥的结构特征，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
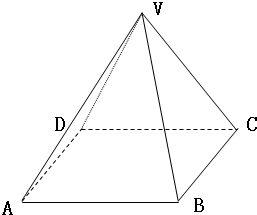如图，以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz，其中Ox∥BC，Oy∥AB；已知VA=kAB，点E是VC的中点，底面正方形ABCD边长为2a，高为h．
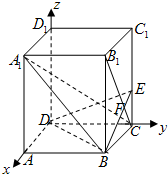已知正四棱柱ABCD-A1B1C1D1底面边长AB=2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交线段B1C于点F．以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D-xyz，如图．
我们将底面是正方形，侧棱长都相等的棱锥称为正四棱锥．已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同，且如图所示，视图中四边形ABCD是边长为1的正方形，则该几何体的体积为（ ）