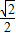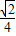题目内容
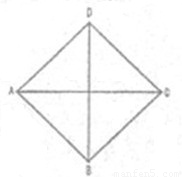
 我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )
我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )分析:由三视图可知:该几何体是由两个同底面正四棱锥组成的如图所示的几何体,其所有棱长都为1.据此即可计算出体积.
解答:解:由三视图可知:该几何体是由两个同底面正四棱锥组成的如图所示的几何体:
其所有棱长都为1.
∵OE=
EG=
,∴OP=
=
.
∴V=2×
×12×
=
.
故选C.

其所有棱长都为1.
∵OE=
| 1 |
| 2 |
| ||
| 2 |
1-(
|
| ||
| 2 |
∴V=2×
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
故选C.
点评:由三视图正确恢复原几何体是解题的关键.

练习册系列答案
相关题目