题目内容
在直角坐标系xOy中,设动点P到直线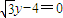 的距离为d1,到点(0,
的距离为d1,到点(0,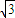 )的距离为d2,且
)的距离为d2,且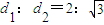 .又设点P的轨迹为C,直线l:y=kx+1与C交于A,B两点.
.又设点P的轨迹为C,直线l:y=kx+1与C交于A,B两点.(Ⅰ)写出轨迹C的方程;
(Ⅱ)若
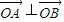 ,求k的值;
,求k的值;(Ⅲ)若点A在第一象限,试问:当k>0时,是否恒有
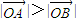 ?
?
【答案】分析:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以(0,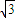 )为焦点,以直线
)为焦点,以直线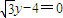 为准线的椭圆.由此能求出曲线C的方程.
为准线的椭圆.由此能求出曲线C的方程.
(Ⅱ)由 ,得(k2+4)x2+2kx-3=0.设A(x1,y1),B(x2,y2),故
,得(k2+4)x2+2kx-3=0.设A(x1,y1),B(x2,y2),故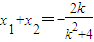 ,
,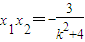 .若
.若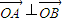 ,即x1x2+y1y2=0.由此能求出k的值.
,即x1x2+y1y2=0.由此能求出k的值.
(Ⅲ)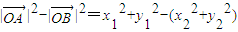 =
= .因为A在第一象限,故x1>0.由
.因为A在第一象限,故x1>0.由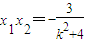 ,知x2<0,由此计k>0时,
,知x2<0,由此计k>0时,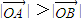 .
.
解答:解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以(0,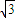 )为焦点,以直线
)为焦点,以直线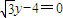 为准线的椭圆.
为准线的椭圆.
由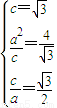 得
得 ,故曲线C的方程为
,故曲线C的方程为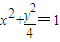 .…(4分)
.…(4分)
(Ⅱ)由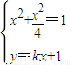 ,消去y并整理得(k2+4)x2+2kx-3=0.
,消去y并整理得(k2+4)x2+2kx-3=0.
设A(x1,y1),B(x2,y2),
故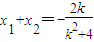 ,
,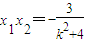 .
.
若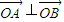 ,即x1x2+y1y2=0.
,即x1x2+y1y2=0.
而y1y2=k2x1x2+k(x1+x2)+1,
于是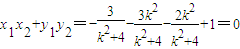 ,
,
化简得-4k2+1=0,
所以k=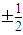 .….(8分)
.….(8分)
(Ⅲ)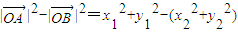
=(x12-x22)+4(1-x12-1+x22)
=-3(x1-x2)(x1+x2)
=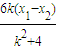 .
.
因为A在第一象限,故x1>0.
由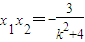 ,知x2<0,
,知x2<0,
从而x1-x2>0.又k>0,
故 ,
,
即在题设条件下,恒有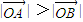 .…(12分)
.…(12分)
点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.
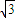 )为焦点,以直线
)为焦点,以直线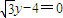 为准线的椭圆.由此能求出曲线C的方程.
为准线的椭圆.由此能求出曲线C的方程.(Ⅱ)由
 ,得(k2+4)x2+2kx-3=0.设A(x1,y1),B(x2,y2),故
,得(k2+4)x2+2kx-3=0.设A(x1,y1),B(x2,y2),故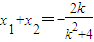 ,
,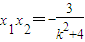 .若
.若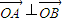 ,即x1x2+y1y2=0.由此能求出k的值.
,即x1x2+y1y2=0.由此能求出k的值.(Ⅲ)
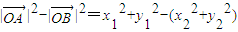 =
= .因为A在第一象限,故x1>0.由
.因为A在第一象限,故x1>0.由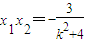 ,知x2<0,由此计k>0时,
,知x2<0,由此计k>0时,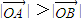 .
.解答:解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以(0,
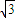 )为焦点,以直线
)为焦点,以直线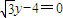 为准线的椭圆.
为准线的椭圆.由
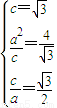 得
得 ,故曲线C的方程为
,故曲线C的方程为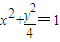 .…(4分)
.…(4分)(Ⅱ)由
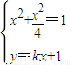 ,消去y并整理得(k2+4)x2+2kx-3=0.
,消去y并整理得(k2+4)x2+2kx-3=0.设A(x1,y1),B(x2,y2),
故
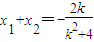 ,
,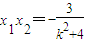 .
.若
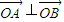 ,即x1x2+y1y2=0.
,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,
于是
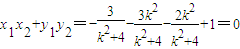 ,
,化简得-4k2+1=0,
所以k=
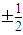 .….(8分)
.….(8分)(Ⅲ)
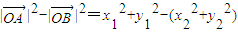
=(x12-x22)+4(1-x12-1+x22)
=-3(x1-x2)(x1+x2)
=
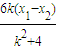 .
.因为A在第一象限,故x1>0.
由
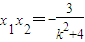 ,知x2<0,
,知x2<0,从而x1-x2>0.又k>0,
故
 ,
,即在题设条件下,恒有
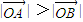 .…(12分)
.…(12分)点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为