题目内容
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2| 3 |
(1)求线段PQ中点M的轨迹C的方程;
(2)R1,R2是曲线C上的动点,R1,R2到y轴的距离之和为1,设u为R1,R2到x轴的距离之积.问:是否存在最大的常数m,使u≥m恒成立?若存在,求出这个m的值;若不存在,请说明理由.
分析:(1)求出OA的方程,设出M(x,y),P(a,
a),Q(0,b),利用中点坐标公式,三角形的面积公式,消去a,b得点M的轨迹C的方程.
(2)设R1(x1,y1),R2(x2,y2),则x1+x2=1,推出u的表达式,令t=x1•x2则0<t≤
,推出u=3(t+
-2),利用导数判断函数的单调性,求出最大的常数m=
使u≥m恒成立.
| 3 |
(2)设R1(x1,y1),R2(x2,y2),则x1+x2=1,推出u的表达式,令t=x1•x2则0<t≤
| 1 |
| 4 |
| 2 |
| t |
| 75 |
| 4 |
解答:解:(1)射线OA:y=
x(x>0).(1分)
设M(x,y),P(a,
a),Q(0,b)(a>0,b>0),
则a=2x,
a+b=2y,(3分)
又因为△POQ的面积为2
,
所以ab=4
;(4分)
消去a,b得点M的轨迹C的方程为:
x2-xy+
=0(x>0,y>0).(7分)
(2)设R1(x1,y1),R2(x2,y2),则x1+x2=1,(8分)
所以u=y1y2=
(x1+
)•
(x2+
)
=3(x1•x2+
+
+
)=3(x1•x2+
-2)(9分)
令t=x1•x2则0<t≤
,所以有u=3(t+
-2),(11分)
则有:当0<t≤
时,u/=3(1-
)<0,
所以u=3(t+
-2)在(0,
]上单调递减,
所以当t=
时,umin=
,(13分)
所以存在最大的常数m=
使u≥m恒成立.(14分)
| 3 |
设M(x,y),P(a,
| 3 |
则a=2x,
| 3 |
又因为△POQ的面积为2
| 3 |
所以ab=4
| 3 |
消去a,b得点M的轨迹C的方程为:
| 3 |
| 3 |
(2)设R1(x1,y1),R2(x2,y2),则x1+x2=1,(8分)
所以u=y1y2=
| 3 |
| 1 |
| x1 |
| 3 |
| 1 |
| x2 |
=3(x1•x2+
| 1 |
| x1•x2 |
| x2 |
| x1 |
| x1 |
| x2 |
| 2 |
| x1•x2 |
令t=x1•x2则0<t≤
| 1 |
| 4 |
| 2 |
| t |
则有:当0<t≤
| 1 |
| 4 |
| 2 |
| t2 |
所以u=3(t+
| 2 |
| t |
| 1 |
| 4 |
所以当t=
| 1 |
| 4 |
| 75 |
| 4 |
所以存在最大的常数m=
| 75 |
| 4 |
点评:本题中档题,考查与直线有关的函数的最值问题曲线的轨迹方程的求法,导数的应用,单调性常常利用导数求解;考查计算能力,转化思想,是有难度的中档题,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
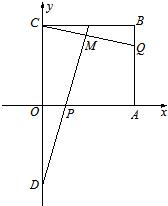 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2, (2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
(2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB. ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.
 ,点P,Q满足
,点P,Q满足 ,
, ,点D是C关于原点的对称点,直线DP与CQ相交于点M.
,点D是C关于原点的对称点,直线DP与CQ相交于点M.